
【题目】如图所示,已知椭圆![]() 过点
过点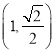 ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,点
,点![]() 为直线
为直线![]() 上且不在
上且不在![]() 轴上的任意一点,直线
轴上的任意一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 为坐标原点.
为坐标原点.
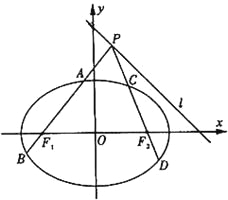
(1)求椭圆的标准方程;
(2)设直线![]() 、
、![]() 的斜线分别为
的斜线分别为![]() 、
、![]() .
.
(i)证明:![]() ;
;
(ii)问直线![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率
的斜率![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足![]() ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)(i)见解析;(ii)
;(2)(i)见解析;(ii)![]()
【解析】
(1)利用椭圆过已知点和离心率,联立方程求得a和b,则椭圆的方程可得;
(2)(i)把直线PF1、PF2的方程联立求得交点的坐标,代入直线x+y=2上,整理得![]() ;
;
(ii)设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+kOB+kOC+kOD=0推断出k1+k2=0或k1k2=1,分别讨论求得p.
(1)∵椭圆过点![]() ,
,![]() ,∴
,∴![]() ,故所求椭圆方程为
,故所求椭圆方程为![]() ;
;
(2)(i)由于F1(﹣1,0)、F2(1,0),PF1,PF2的斜率分别是k1,k2,且点P不在x轴上,
所以k1≠k2,k1≠0,k2≠0.又直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x﹣1),
联立方程解得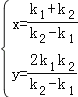 ,所以
,所以![]() ,由于点P在直线x+y=2上,
,由于点P在直线x+y=2上,
所以![]() ,故
,故![]()
(ii)设A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),联立直线PF1和椭圆的方程得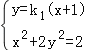 ,化简得(2k12+1)x2+4k12x+2k12﹣2=0,
,化简得(2k12+1)x2+4k12x+2k12﹣2=0,
因此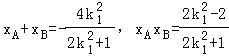 ,所以
,所以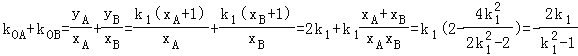 ,
,
同理可得: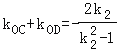 ,故由kOA+kOB+kOC+kOD=0得k1+k2=0或k1k2=1,
,故由kOA+kOB+kOC+kOD=0得k1+k2=0或k1k2=1,
当k1+k2=0时,由(1)的结论可得k2=﹣2,解得P点的坐标为(0,2)
当k1k2=1时,由(1)的结论可得k2=3或k2=﹣1(舍去),
此时直线CD的方程为y=3(x﹣1)与x+y=2联立得x=![]() ,
,![]() ,所以
,所以![]() ,
,
综上所述,满足条件的点P的坐标分别为![]() ,P(0,2).
,P(0,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,离心率是
,离心率是![]() ,直线
,直线![]() 过点
过点![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,
时, ![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当直线![]() 绕点
绕点![]() 运动时,试求
运动时,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一元线性同余方程组问题最早可见于中国南北朝时期(公元![]() 世纪)的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即,一个整数除以三余二,除以五余三,求这个整数.设这个整数为
世纪)的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即,一个整数除以三余二,除以五余三,求这个整数.设这个整数为![]() ,当
,当![]() 时, 符合条件的
时, 符合条件的![]() 共有_____个.
共有_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,设点
中,设点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,过
轴的交点,过![]() 、
、![]() 分别作直线
分别作直线![]() 、
、![]() ,使
,使![]() ,
,![]() ,
,![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知⊙![]() :
:![]() ,过抛物线
,过抛物线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于
相切于![]() 、
、![]() 两点,若直线
两点,若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 。
。![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中的数所成的数列,它包含
中的数所成的数列,它包含![]() 的不以1结尾的任何排列,即对于
的不以1结尾的任何排列,即对于![]() 的四个数的任意一个不以1结尾的排列
的四个数的任意一个不以1结尾的排列![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,并且
,并且![]() ,求这种数列的项数
,求这种数列的项数![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①函数![]() 的单调增区间是
的单调增区间是![]() ;
;
②若函数![]() 定义域为
定义域为![]() 且满足
且满足![]() ,则它的图象关于
,则它的图象关于![]() 轴对称;
轴对称;
③函数![]() 的值域为
的值域为![]() ;
;
④函数![]() 的图象和直线
的图象和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值可能是
的值可能是![]() ;
;
⑤若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中正确的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com