
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | p∨(¬q) |
分析 先根据向量的数量判断命题p为假命题,再根据偶函数的定义判断出命题q为真命题,最后根据复合命题的真假判断即可.
解答 解:∵向量$\overrightarrow{a}$=(1,2)与向量$\overrightarrow{b}$=(2,k)的夹角为锐角,
∴$\overrightarrow{a}•\overrightarrow{b}$=2+2k>0,解得k>-1,
当k=4时,$\overrightarrow{a}$=$\frac{1}{2}$$\overrightarrow{b}$,则$\overrightarrow{a}$与$\overrightarrow{b}$共线,
即向量$\overrightarrow{a}$=(1,2)与向量$\overrightarrow{b}$=(2,k)的夹角为锐角的充要条件是k>-1且k≠4,
∴命题p为假命题,
∵函数f(x)=$\left\{\begin{array}{l}sin(x+\frac{π}{3}),x≤0\\ cos(x+\frac{π}{6}),x>0\end{array}$,
∴f(-x)=$\left\{\begin{array}{l}{sin(-x+\frac{π}{3}),-x≤0}\\{cos(-x+\frac{π}{6}),-x>0}\end{array}\right.$=$\left\{\begin{array}{l}{cos(x+\frac{π}{6}),x≥0}\\{sin(x+\frac{π}{3}),x<0}\end{array}\right.$=f(x),
∴f(x)为偶函数,
∴命题q为真命题,
∴¬p∧q为真命题,
故选:B.
点评 本题考查了向量的夹角公式和偶函数的定义,因复合命题的判断,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
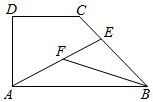 如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.
如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | {0,1,2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com