
分析 (1)根据函数的单调性,得到g(1)=1,g(3)=5,求出a,b的值即可;
(2)(1)由函数g(x)=a(x-1)2+1+b-a,a>0,所以g(x)在区间[2,3]上是增函数,得到方程组,由此解得a、b的值,
(3)方程f(|2k-1|)+k•$\frac{2}{{|2}^{k}-1|}$-3k=0⇒|2x-1|2-(2+3k)|2x-1|+(2+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(2+2k)=0(t≠0),构造函数h(t)=t2-(2+3k)t+(2+2k),通过数形结合与等价转化的思想即可求得k的范围.
解答 解:(1)g(x)=a(x-1)2+1+b-a,
因为a>0,所以g(x)在区间(0,1]上是减函数,[1,3]上是增函数,
故$\left\{\begin{array}{l}g(1)=1\\ g(3)=5\end{array}\right.$,解得$\left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$.
(2)由已知可得$f(x)=x+\frac{2}{x}-2$,
所以f(2x)-k•2x≥0可化为${2^x}+\frac{2}{2^x}-2≥k•{2^x}$,
化为$1+2{({\frac{1}{2^x}})^2}-2•\frac{1}{2^x}≥k$,令$t=\frac{1}{2^x}$,则k≤2t2-2t+1,
因x∈[-1,1],故$t∈[{\frac{1}{2}\;,\;2}]$,
记h(t)=2t2-2t+1,
因为$t∈[{\frac{1}{2},2}]$,故$h{(t)_{min}}=h(\frac{1}{2})=\frac{1}{2}$,
∴k≤$\frac{1}{2}$;
(3)方程f(|2x-1|)+k•$\frac{2}{{|2}^{x}-1|}$-3k=0可化为:
|2x-1|2-(2+3k)|2x-1|+(2k+2)=0,|2x-1|≠0,
令|2x-1|=t,则方程化为
t2-(2+3k)t+(2k+2)=0(t≠0),
∵方程f(|2x-1|)+k•$\frac{2}{{|2}^{x}-1|}$-3k=0有三个不同的实数解,
∴由t=|2x-1|的图象知,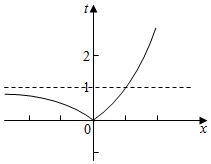
t2-(2+3k)t+(2+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记h(t)=t2-(2+3k)t+(2+2k),
则 $\left\{\begin{array}{l}{h(0)=2k+2>0}\\{h(1)=1-k<0}\end{array}\right.$,或 $\left\{\begin{array}{l}{h(0)=2+2k>0}\\{h(1)=1-k=0}\\{0<\frac{2+3k}{2}<1}\end{array}\right.$,
∴k>1.
点评 本题考查二次函数在闭区间上的最值,考查函数恒成立问题问题,考查数形结合与等价转化、函数与方程思想的综合应用,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,0] | B. | [2-2$\sqrt{2}$,2+2$\sqrt{2}$] | C. | [0,4] | D. | [-2-2$\sqrt{2}$,-2+2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值-1 | B. | 最大值14 | C. | 最大值9 | D. | 最大值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤3} | B. | {x|-2≤x≤3} | C. | {x|1<x≤3} | D. | {x|-2≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com