
【题目】写出下面平面几何中的常见结论在立体几何中也成立的所有序号______.
①四边形内角和为![]() ;
;
②垂直的两条直线必相交;
③垂直同一条直线的两条直线平行;
④平行同一条直线的两条直线平行;
⑤四边相等的四边形,其对角线垂直;
⑥到三角形三边距离相等的点是这个三角形的内心;
⑦到一个角的两边距离相等的点必在这个角的角平分线上;
⑧在平面几何中有“一组平行线(至少3条)被两条直线所截得的对应线段成比例”的结论,则这一结论可推广到立体几何中“一组平行平面(至少3个)被两条直线所截得的对应线段也成比例.”
【答案】④⑤⑧
【解析】
①将长方形沿对角线对折,则四边形内角和不为![]() ;②这两条直线可能异面;③正方体的同一顶点的三条棱相互垂直;④是公理,正确;⑤四边相等的四边形也可能是空间四边形,对角线不一定垂直;⑥过三角形的内心且垂直于三角形所在平面的直线上的点到各边的距离都相等;⑦过这个角的角平分线与角所在平面垂直的平面的点到这个角的两边距离相等,故不正确;⑧正确
;②这两条直线可能异面;③正方体的同一顶点的三条棱相互垂直;④是公理,正确;⑤四边相等的四边形也可能是空间四边形,对角线不一定垂直;⑥过三角形的内心且垂直于三角形所在平面的直线上的点到各边的距离都相等;⑦过这个角的角平分线与角所在平面垂直的平面的点到这个角的两边距离相等,故不正确;⑧正确
①将长方形沿对角线对折,则四边形内角和不为![]() ,故①不正确;
,故①不正确;
②这两条异面直线垂直时不相交,故②不正确;
③正方体的同一顶点的三条棱相互垂直,故③不正确;
④是公理,故④正确;
⑤四边相等的四边形若是平面图形,可得其必是菱形,结论正确,若四边相等的四边形是空间四边形,一条对角线与另一条对角线所在面垂直,可得两对角线一定垂直,故⑤正确;
⑥过三角形的内心且垂直于三角形所在平面的直线上的点到各边的距离都相等,故⑥不正确;
⑦过这个角的角平分线与角所在平面垂直的平面的点到这个角的两边距离相等,故⑦不正确;
⑧当两条直线平行时易证结论成立,当两条直线异面时,可作第三条直线与其中一条直线平行,与另一条直线相交,可证明成立,故⑧正确.
故答案为:④⑤⑧


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】己知椭圆C:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,直线l:
,直线l:![]() 与椭圆C交于A,B两点
与椭圆C交于A,B两点![]() 为坐标原点.
为坐标原点.
![]() 若直线l过点
若直线l过点![]() ,且
,且![]() 十
十![]() ,求直线l的方程;
,求直线l的方程;
![]() 若以AB为直径的圆过点O,点P是线段AB上的点,满足
若以AB为直径的圆过点O,点P是线段AB上的点,满足![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于![]() 分的选手定为合格选手,直接参加第二轮比赛,大于等于
分的选手定为合格选手,直接参加第二轮比赛,大于等于![]() 分的选手将直接参加竞赛选拔赛.已知成绩合格的
分的选手将直接参加竞赛选拔赛.已知成绩合格的![]() 名参赛选手成绩的频率分布直方图如图所示,其中
名参赛选手成绩的频率分布直方图如图所示,其中![]() 的频率构成等比数列.
的频率构成等比数列.
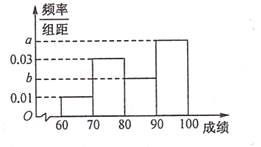
(1)求![]() 的值;
的值;
(2)估计这![]() 名参赛选手的平均成绩;
名参赛选手的平均成绩;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为![]() ,假设每名选手能否通过竞赛选拔赛相互独立,现有
,假设每名选手能否通过竞赛选拔赛相互独立,现有![]() 名选手进入竞赛选拔赛,记这
名选手进入竞赛选拔赛,记这![]() 名选手在竞赛选拔赛中通过的人数为随机变量
名选手在竞赛选拔赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.

(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位
平均增加5个单位
③线性回归方程![]() 必过
必过![]()
④设具有相关关系的两个变量![]() 的相关系数为
的相关系数为![]() ,那么
,那么![]() 越接近于0,
越接近于0,![]() 之间的线性相关程度越高;
之间的线性相关程度越高;
⑤在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,那么
的值,那么![]() 的值越大,判断两个变量间有关联的把握就越大。
的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且
,且![]() 过点
过点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆,经过点
为直径的圆,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com