
����Ŀ��Ϊ�˼����������ij��������������Ӳ�Ʒ�������ȡ100�������������ߴ磬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��������ߴ���������![]() ֮�ڣ�����Ϊ������ϸ�����Ϊ���ϸ�����
֮�ڣ�����Ϊ������ϸ�����Ϊ���ϸ�����![]() ��
��![]() �ֱ��ʾ������ƽ��ֵ�ͱ�������
�ֱ��ʾ������ƽ��ֵ�ͱ�������![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
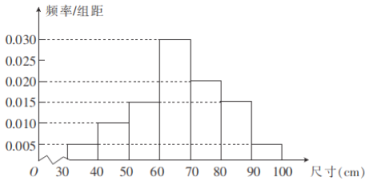
��1����֪һ������ijߴ���![]() �����жϸ�����Ƿ�ϸ�
�����жϸ�����Ƿ�ϸ�
��2�����÷ֲ�����ķ����ӳߴ���![]() �������г�ȡ6��������ٴ���6������������ȡ2��������2�������ǡ��1���ߴ�С��
�������г�ȡ6��������ٴ���6������������ȡ2��������2�������ǡ��1���ߴ�С��![]() �ĸ��ʣ�
�ĸ��ʣ�
���𰸡���1����������ϸ�2��![]()
��������
��1������Ƶ�ʷֲ�ֱ��ͼ�������![]() �����䣬���ж�
�����䣬���ж�![]() �Ƿ����������ڣ����ɵô𰸣�
�Ƿ����������ڣ����ɵô𰸣�
��2������6��������Ϊ��![]() �����г�����6������������ȡ2���Ļ����¼������¼�
�����г�����6������������ȡ2���Ļ����¼������¼�![]() Ϊ����ѡ����2�������ǡ��1���ߴ�С��
Ϊ����ѡ����2�������ǡ��1���ߴ�С��![]() ���������¼�
���������¼�![]() �����Ļ����¼������ùŵ���ͼ�����ʣ����ɵô𰸣�
�����Ļ����¼������ùŵ���ͼ�����ʣ����ɵô𰸣�
��1���Ǹ����Ƶ��Ϊ![]() ���������
���������
![]() ��
��
![]()
��![]()
![]()
��![]()
��![]() ���ʸ�������ϸ�
���ʸ�������ϸ�
��2����ǰ�����ȡ����������ֱ�Ϊ![]()
��![]() ����
����![]()
���ȡ����6������гߴ�С��![]() ����3����
����3����
����6����������![]() ������
������![]() Ϊ�ߴ�С��
Ϊ�ߴ�С��![]() �ģ�
�ģ�
���¼�![]() Ϊ����ѡ����2�������ǡ��1���ߴ�С��
Ϊ����ѡ����2�������ǡ��1���ߴ�С��![]() ��
��
�����6������������ȡ2���Ļ����¼��У�
![]()
![]() ��15����
��15����
���¼�![]() �����Ļ����¼��У�
�����Ļ����¼��У�
![]() ��9��
��9��
��![]()
����2�������ǡ��1���ߴ�С��![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��
��


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ���жϲ�˵������
ʱ���жϲ�˵������![]() ��������.������
��������.������![]() ��������������
��������������![]()
![]() �ڣ���
�ڣ���![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��������������
��������������![]() ��ʹ�öԶ������ڵ�ÿһ��ֵ
��ʹ�öԶ������ڵ�ÿһ��ֵ![]() �����䶨�����ڶ�����
�����䶨�����ڶ�����![]() ��ʹ
��ʹ![]() ����������Ƹú���Ϊ��������������
����������Ƹú���Ϊ��������������
��1���ֱ��жϺ�����![]() ����
����![]() �Ƿ�Ϊ����������������˵�����ɣ�
�Ƿ�Ϊ����������������˵�����ɣ�
��2��������![]() ��ֵ��Ϊ
��ֵ��Ϊ![]() ����֤����
����֤����![]() �����������������ij�Ҫ��������
�����������������ij�Ҫ��������![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������![]() �У��ı���
�У��ı���![]() Ϊ���Σ�
���� ![]() ����
����![]() .��
.��![]() �����ƽ���Ϊ
�����ƽ���Ϊ![]() ��
�� ![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() .
.
(I)֤���� ![]() Ϊ
Ϊ![]() ���е㣻
���е㣻
(II)�����������ƽ��![]() ���ֳ����������ֵ����֮��.
���ֳ����������ֵ����֮��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�ǵ��������ĵȲ����У�a2+a4��14��a2��1��a3+1��a4+7�ɵȱ����У�
��1��������{an}��ͨ�ʽ��
��2��������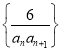 ��ǰn���ΪSn��
��ǰn���ΪSn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1��![]() ������
������![]() �ĵ������䣺
�ĵ������䣺
��2����������![]() ������ʽ
������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ĵ���
�ĵ���![]() �DZ߳�
�DZ߳�![]() �����Σ�
������![]() ��
��![]() ���е�
���е�![]() �Ƕ���
�Ƕ���![]() �ڵ���
�ڵ���![]() ����Ӱ��
����Ӱ��![]() ��
��![]() ���е�.
���е�.

(1)��֤����![]() ƽ��
ƽ��![]() ��
��
(2)��![]() �������
�������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������סԺ��������ҽԺ�������εIJ�������ʱ�ͻᷢ����ҽ����Դ���ҡ��������¹ڷ��ױ����ڼ䣬����ij��ÿ���°��ͳ��סԺ���������з��֣�����ÿ�����¹ڷ���סԺ��������ǰһ���°��ͳ�Ƶ�סԺ��������Լ25%����ÿ�մ�Լ��200���¹ڷ�����������Ժ����֪����ij���°����1000���¹ڷ�����סԺ���ƣ����е�ҽԺ��������4000���¹ڷ����ߣ����������������Ĺ��ɷ�չ���������¹ڷ������鷢����ҽ����Դ���ҡ�����ֻ��ҪԼ�� ��
�ο����ݣ�![]() .
.
A.7��B.10��C.13��D.16��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com