
已知点 是抛物线
是抛物线 上不同的两点,点
上不同的两点,点 在抛物线
在抛物线 的准线
的准线 上,且焦点
上,且焦点
 到直线
到直线 的距离为
的距离为 .
.
(I)求抛物线 的方程;
的方程;
(2)现给出以下三个论断:①直线 过焦点
过焦点 ;②直线
;②直线 过原点
过原点 ;③直线
;③直线 平行
平行 轴.
轴.
请你以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题,并加以证明.
(1) ;(2)参考解析
;(2)参考解析
【解析】
试题分析:(1)由点F到直线 的距离为
的距离为 可求得抛物线中
可求得抛物线中 .从而得到抛物线方程.
.从而得到抛物线方程.
(2)根据题意共有三种情况:i) ①直线 过焦点
过焦点 ;②直线
;②直线 过原点
过原点 .由直线AB与抛物线的方程联立结合韦达定理,表示出点D,B的坐标即可得到③直线
.由直线AB与抛物线的方程联立结合韦达定理,表示出点D,B的坐标即可得到③直线 平行
平行 轴.ii) ①直线
轴.ii) ①直线 过焦点
过焦点 ;③直线
;③直线 平行
平行 轴同样是表达出点D,B的坐标即可得到点A,O,D三点共线,即可得到结论.iii) ②直线
轴同样是表达出点D,B的坐标即可得到点A,O,D三点共线,即可得到结论.iii) ②直线 过原点
过原点 ;③直线
;③直线 平行
平行 轴表达出点A,B的坐标关系即可得到点A,F,B三点共线,即得到结论.
轴表达出点A,B的坐标关系即可得到点A,F,B三点共线,即得到结论.
(I)因为 , 依题意得
, 依题意得 , 2分
, 2分
解得 ,所以抛物线
,所以抛物线 的方程为
的方程为 4分
4分
(2)①命题:若直线 过焦点
过焦点 ,且直线
,且直线 过原点
过原点 ,则直线
,则直线 平行
平行 轴.
轴.
5分
设直线 的方程为
的方程为 ,
, , 6分
, 6分
由 得
得 ,
,
 , 8分
, 8分
直线 的方程为
的方程为 , 9分
, 9分
所以点 的坐标为
的坐标为 ,
,
 , 12分
, 12分
 直线
直线 平行于
平行于 轴. 13分
轴. 13分
②命题:若直线 过焦点
过焦点 ,且直线
,且直线 平行
平行 轴,则直线
轴,则直线 过原点
过原点 .
.
5分
设直线 的方程为
的方程为 ,
, , 6分
, 6分
由 得
得 ,
,
 , 8分
, 8分
即点 的坐标为
的坐标为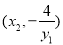 , 9分
, 9分
∵直线 平行
平行 轴,∴点
轴,∴点 的坐标为
的坐标为 , 10分
, 10分
∴ ,
, ,
,
由于 ,
,
∴ ∥
∥ ,即
,即 三点共线, 12分
三点共线, 12分
∴直线 过原点
过原点 . 13分
. 13分
③命题:若直线 过原点
过原点 ,且直线
,且直线 平行
平行 轴,则直线
轴,则直线 过焦点
过焦点 . 5分
. 5分
设直线 的方程为
的方程为 ,则点
,则点 的坐标为
的坐标为 , 6分
, 6分
∵直线 平行
平行 轴,
轴,
∴ ,∴
,∴ ,即点
,即点 的坐标为
的坐标为 , 8分
, 8分
由 得
得 ,
,
∴ 即点
即点 的坐标为
的坐标为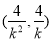 , 10分
, 10分
∴ ,
,
由于 ,
,
∴ ∥
∥ ,即
,即 三点共线, 12分
三点共线, 12分
∴直线 过焦点
过焦点 . 13分
. 13分
考点:1.抛物线的性质.2.直线与抛物线位置关系.3.韦达定理的应用.4.三点共线的判定.


科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:选择题
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2 的等腰三角腰形,则该几何体的体积是( )
A. B.
B. C.
C. D.4
D.4

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
在 中,
中,  是
是 边上的高,给出下列结论:
边上的高,给出下列结论:
①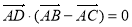 ; ②
; ② ; ③
; ③ ;
;
其中结论正确的个数是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
已知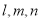 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,下列命题为真命题的是 ( )
是两个不同的平面,下列命题为真命题的是 ( )
A.若 ,
, ,
, ,
, ,则
,则
B.若 ,
, ∥
∥ ,
, ,则
,则
C.若 ∥
∥ ,
, ,则
,则 ∥
∥
D.若 ,
, ,
, ,则
,则 ∥
∥
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)求不等式 的解集
的解集 ;
;
(2)若存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
设 且
且 ,命题
,命题 :函数
:函数 在
在 上是增函数 ,命题
上是增函数 ,命题 :函数
:函数 在
在 上是减函数,则
上是减函数,则 是
是 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:选择题
在边长为2的等边 中,
中, 是
是 的中点,
的中点, 为线段
为线段 上一动点,则
上一动点,则 的取值范
的取值范
围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练六(解析版) 题型:选择题
已知集合A={x|x>1},B={x|x<m},且A∪B=R,那么m的值可以是( )
A.-1 B.0 C.1 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com