
分析 (Ⅰ)若a=b=1,求出函数F(x)=f(x)-g(x)的导数,判断函数在定义域上单调递增,利用函数单调性和最值之间的关系进行求解即可;
(Ⅱ)设x1<x2,根据条件得到x2-x1=a(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)(${e}^{{x}_{2}}$+${e}^{{x}_{1}}$)+b(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$),再令t=x2-x1>0,则设G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t,利用导数得出函数为增函数,继而得出即f′(x0)<1,而g′(x0)=1,进行比较即可.
解答 解:(I)若a=b=1,则F(x)=f(x)-g(x)=e2x+ex-x,
则F′(x)=2e2x+ex-1=(ex+1)(2ex-1),
由F′(x)>0得(ex+1)(2ex-1)>0,得2ex-1>0得ex>$\frac{1}{2}$,则x>ln$\frac{1}{2}$,
由F′(x)<0得(ex+1)(2ex-1)<0,得2ex-1<0得ex<$\frac{1}{2}$,则x<ln$\frac{1}{2}$,
故当x=ln$\frac{1}{2}$时,函数F(x)取得极小值同时也是最小值,此时F(ln$\frac{1}{2}$)=$\frac{3}{4}$-ln$\frac{1}{2}$.
(Ⅱ)不妨设x1<x2,则$\frac{{x}_{2}+{x}_{1}}{2}$=x0,
$a{e}^{2{x}_{1}}$+$b{e}^{{x}_{1}}$=x1,a${e}^{2{x}_{2}}$+b${e}^{{x}_{2}}$=x2,
两式相减得:a(${e}^{2{x}_{2}}$-${e}^{2{x}_{1}}$)+b(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)=x2-x1,
整理得x2-x1=a(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)(${e}^{{x}_{2}}$+${e}^{{x}_{1}}$)+b(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)
则$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$=a(${e}^{{x}_{2}}$+${e}^{{x}_{1}}$)+b≥2a${e}^{\frac{{x}_{2}+{x}_{1}}{2}}$+b,
于是$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$•${e}^{\frac{{x}_{2}+{x}_{1}}{2}}$≥2a${e}^{{x}_{2}+{x}_{1}}$+b${e}^{\frac{{x}_{2}+{x}_{1}}{2}}$=f′(x0)
而是$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$•${e}^{\frac{{x}_{2}+{x}_{1}}{2}}$=$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}-{x}_{1}}-1}$•${e}^{\frac{{x}_{2}-{x}_{1}}{2}}$
令t=x2-x1>0,则设G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t,
则G′(t)$\frac{1}{2}$=${e}^{\frac{t}{2}}$+$\frac{1}{2}$${e}^{-\frac{t}{2}}$-1>$\frac{1}{2}$×2$\sqrt{{e}^{\frac{t}{2}}•{e}^{-\frac{t}{2}}}$-1=0,
∴y=G(t)在(0,+∞)上单调递增,
则G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t>G(0),
于是有${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$>t,
即et-1$>t•{e}^{\frac{t}{2}}$,且et-1>0,
∴$\frac{t}{{e}^{t}-1}•{e}^{\frac{t}{2}}$<1,
即f′(x0)<1.
∵g(x)=x,
∴g′(x0)=1,则f′(x0)<g′(x0).
点评 本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,考查学生本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,考查学生分析解决问题的能力,属于难题分析解决问题的能力,属于难题


科目:高中数学 来源: 题型:填空题
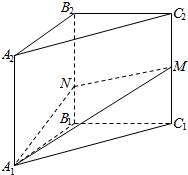 如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.
如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com