
分析 (1)计算bn+1-bn=$\frac{{a}_{n}-{a}_{n+1}}{({a}_{n+1}-1)({a}_{n}-1)}$=$\frac{1}{3}$;
(2)求出bn的通项公式,得出Tn,使用错位相减法求和.
解答 解:(1)∵$\frac{({a}_{n+1}-1)({a}_{n}-1)}{{a}_{n}-{a}_{n+1}}$=3,∴$\frac{{a}_{n}-{a}_{n+1}}{({a}_{n+1}-1)({a}_{n}-1)}$=$\frac{1}{3}$,∴bn+1-bn=$\frac{1}{{a}_{n+1}-1}$-$\frac{1}{{a}_{n}-1}$=$\frac{{a}_{n}-{a}_{n+1}}{({a}_{n+1}-1)({a}_{n}-1)}$=$\frac{1}{3}$.
∴数列{bn}是等差数列.
(2)b1=$\frac{1}{{a}_{1}-1}$=$\frac{1}{2}$,∴bn=$\frac{1}{2}$+$\frac{1}{3}$(n-1)=$\frac{1}{3}$n+$\frac{1}{6}$.
∴Tn=2•$\frac{1}{2}$+22•$\frac{5}{6}$+23•$\frac{7}{6}$+24•$\frac{9}{6}$+…+2n•$\frac{2n+1}{6}$,①
①×2得:2Tn=22•$\frac{1}{2}$+23•$\frac{5}{6}$+24•$\frac{7}{6}$+25•$\frac{9}{6}$+…+2n+1•$\frac{2n+1}{6}$,②
①-②得:-Tn=1+$\frac{1}{3}•{2}^{2}$+$\frac{1}{3}•{2}^{3}$+$\frac{1}{3}•{2}^{4}$+…+$\frac{1}{3}$•2n-2n+1•$\frac{2n+1}{6}$=1-2n+1•$\frac{2n+1}{6}$+$\frac{1}{3}$•$\frac{4(1-{2}^{n-1})}{1-2}$=1-2n+1•$\frac{2n+1}{6}$+$\frac{1}{3}$•(2n+1-4)=-$\frac{1}{3}$-$\frac{2n-1}{6}$•2n+1.
∴Tn=$\frac{1}{3}$+$\frac{2n-1}{6}$•2n+1.
点评 本题考查了数列等差关系的判断,数列求和,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
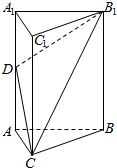 如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.
如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com