
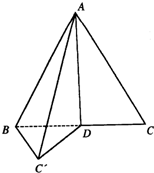
 如图所示,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后点A到直线BC′的距离为
如图所示,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后点A到直线BC′的距离为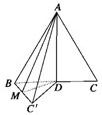 解:如图,作DM⊥BC′于点M,连接AM,则AM为点A到直线BC′的距离,
解:如图,作DM⊥BC′于点M,连接AM,则AM为点A到直线BC′的距离,| 3 |
| 3 |
| AD2+DM2 |
| 15 |
2
| ||
|
| 15 |


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
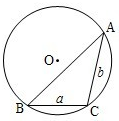 通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.查看答案和解析>>
科目:高中数学 来源: 题型:
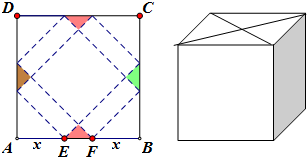 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:044
如图所示,在边长为l的等边△ABC中,⊙O1为△ABC的内切圆.⊙O2与⊙O1外切,且与AB、BC相切,…,⊙On+1与⊙On外切,且与AB、BC相切,如此无限继续下去.记⊙On的面积为an(n∈N*).
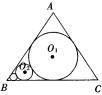
(1)证明{an}是等比数列;
(2)求![]() (a1+a2+…+an)的值
(a1+a2+…+an)的值
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
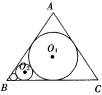
(1)证明{an}是等比数列;
(2)求![]() (a1+a2+…+an)的值
(a1+a2+…+an)的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com