
| ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 |
| ���ijɼ�x | 60 | 70 | 74 | 90 | 94 | 110 |
| ��ʷ�ɼ�y | 58 | 63 | 75 | 79 | 81 | 88 |
���� ��1���ɱ������ݵó����ġ���ʷ�ɼ�Ϊ�����Ƶ�ʣ��Ӷ�����ð����ġ���ʷ�ɼ������������
��2���ɱ������ݼ���$\overline{x}$��$\overline{y}$������ع�ϵ����д�����Իع鷽�̣�
��� �⣺��1���ɱ������ݣ����ijɼ�Ϊ�����Ƶ����$\frac{3}{6}$=$\frac{1}{2}$��
��ʷ�ɼ�Ϊ�����Ƶ����$\frac{2}{6}$=$\frac{1}{3}$��
�ʸð����ijɼ������������48��$\frac{1}{2}$=24��
��ʷ�ɼ����������Ϊ48��$\frac{1}{3}$=16������4�֣�
��2���ɱ������ݿɵã�
$\overline{x}$=$\frac{1}{6}$����60+70+74+90+94+110��=83��
$\overline{y}$=$\frac{1}{6}$����58+63+75+79+81+88��=74������6�֣�
��$\sum_{i=1}^{6}$��xi-$\overline{x}$����yi-$\overline{y}$��=1010��
$\sum_{i=1}^{6}$${{��x}_{i}-\overline{x}��}^{2}$=1678������9�֣�
���Իع�ϵ��Ϊb=$\frac{\sum_{i=1}^{6}{��x}_{i}-\overline{x}��{��y}_{i}-\overline{y}��}{{\sum_{i=1}^{n}{��x}_{i}-\overline{x}��}^{2}}$=$\frac{1010}{1678}$��0.6��
a=74-0.6��83=24.2������11�֣�
����y��x�����Իع鷽��Ϊy=0.6x+24.2������12�֣�
���� ���⿼����Ƶ����Ƶ����Ӧ�����⣬Ҳ���������Իع鷽�̵�Ӧ�����⣬�ǻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{10}$ | B�� | 10 | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ac��bc����a��b | B�� | ��a2��b2����a��b | ||
| C�� | ��a��b��c��0����a+c��b+c | D�� | ��$\sqrt{a}$��$\sqrt{b}$����a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
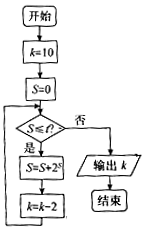
| A�� | 8 | B�� | 6 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
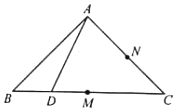 �ڵ���ֱ�ǡ�ABC�У�AB��AC��BC=2��MΪBC�е㣬NΪAC�е㣬DΪBC����һ�����㣬��ABD��AD����ʹBD��DC����A����BCD�ϵ�ͶӰΪ��O������D��BC���˶�ʱ������˵��������ǣ�������
�ڵ���ֱ�ǡ�ABC�У�AB��AC��BC=2��MΪBC�е㣬NΪAC�е㣬DΪBC����һ�����㣬��ABD��AD����ʹBD��DC����A����BCD�ϵ�ͶӰΪ��O������D��BC���˶�ʱ������˵��������ǣ�������| A�� | �߶�NOΪ���� | B�� | $|CO|��[1��\sqrt{2}��$ | C�� | ��AMO+��ADB��180�� | D�� | ��O�Ĺ켣��Բ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}\overrightarrow b+\frac{1}{3}\overrightarrow c$ | B�� | $\frac{1}{3}\overrightarrow b+\frac{2}{3}\overrightarrow c$ | C�� | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ | D�� | $\frac{1}{3}\overrightarrow b-\frac{2}{3}\overrightarrow c$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com