
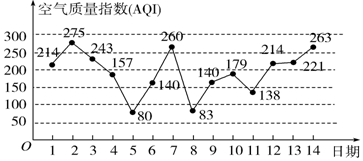
分析 先求出基本事件总数n=12,再求出该同志到达当日空气质量重度污染包含的基本事件个数m=5,由此能求出该同志到达当日空气质量重度污染的概率.
解答 解:某同志随机选择4月1日至4月12日中的某一天到达该市,并停留3天.
基本事件总数n=12,
4月1日至4月12日空气质量重度污染的天数有5天,
即该同志到达当日空气质量重度污染包含的基本事件个数m=5,
∴该同志到达当日空气质量重度污染的概率p=$\frac{m}{n}=\frac{5}{12}$.
故答案为:$\frac{5}{12}$.
点评 本题考查等可能事件的概率计算,涉及到折线图、列举法的运用,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,2018) | B. | (4,2020) | C. | (3,2020) | D. | (2,2020) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | $(1,\frac{{3\sqrt{2}}}{4}]$ | D. | $[\frac{{3\sqrt{2}}}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com