
分析 根据“稳定区间”的定义,我们要想说明函数存在“稳定区间”,我们只要举出一个符合定义的区间M即可,但要说明函数没有“稳定区间”,我们可以用反证明法来说明.由此对四个函数逐一进行判断,即可得到答案.
解答 解:①对于函数f(x)=tan$\frac{π}{4}$x存在“稳定区间”[a,b],
如 x∈[0,1]时,f(x)=tan$\frac{π}{4}$x∈[0,1],
故①是“局部稳定函数”,
②对于函数f(x)=1-x2若存在“稳定区间”[a,b],
如 x∈[0,1]时,f(x)=1-x2∈[0,1],
故②是“局部稳定函数”,
③对于f(x)=ex-1,若存在“稳定区间”[a,b],
由于函数是定义域内的增函数,故有ea-1=a,且eb-1=b,即方程ex-1=x 有两个解,
即y=ex-1和 y=x的图象有两个交点,
这与y=ex-1和 y=x的图象有且只有一个公共点相矛盾,
故③不是“局部稳定函数”,
④对于 f(x)=ln(x-1),若存在“稳定区间”[a,b],
由于函数是定义域内的增函数,故有ln(a-1)=a,且ln(b-1)=b,即方程ln(x-1)=x 有两个解,
即y=ln(x-1)和 y=x的图象有两个交点,
这与y=ln(x-1)和 y=x的图象没有公共点相矛盾,
故④不是“局部稳定函数”,
故答案为:①②
点评 本题以新定义局部稳定函数为载体,考查的知识点是函数的概念及其构造要求,在说明一个函数没有“稳定区间”时,利用函数的性质、图象结合反证法证明是解答本题的关键,属于中档题


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
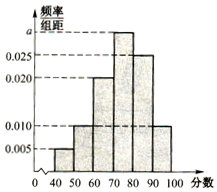 为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.
为了更好的了解某校高三学生期中考试的数学成绩情况,从所有高三学生中抽取40名学生,将他们的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…[90,100]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | $±\sqrt{3}$ | C. | ±2 | D. | $±\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{5},0)$ | B. | $(\frac{2π}{5},0)$ | C. | $(\frac{3π}{5},0)$ | D. | $(\frac{4π}{5},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com