
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 设和直线l平行的直线的方程为x-y+c=0根据点到直线的距离公式和解三角形的有关知识可得符合条件的圆心角的度数为4×30°=120°,根据概率公式计算即可
解答  解:设和直线l平行的直线的方程为x-y+c=0,
解:设和直线l平行的直线的方程为x-y+c=0,
∵圆C上任取一点A到直线l的距离小于1,
∴圆心到直线x-y+c=0的距离小于1,
∴$\frac{|c|}{\sqrt{2}}$≤1,
解得|c|≤$\sqrt{2}$,
分别做直线y=x+$\sqrt{2}$和y=x-$\sqrt{2}$,如图所示,
∵OC=1,OB=2,
∴∠CBO=30°,
∴∠AOB=30°,
∴符合条件的圆心角的度数为4×30°=120°,
根据几何概型的概率公式得到P=$\frac{120}{360}$=$\frac{1}{3}$,
故选:D
点评 本题考查概率的求法,解题时要认真审题,注意圆的性质及点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{3}}}{81}$ | B. | $\frac{{2\sqrt{39}}}{3}$ | C. | $\frac{{26\sqrt{3}}}{3}$ | D. | $2\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
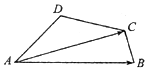 在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com