
 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.分析 (Ⅰ)求导,根据导数的几何意义,求得$\frac{x_0}{p}=1$且${x_0}-\frac{x_0^2}{2p}-\sqrt{2}=0$,即可求得p的值,求得抛物线的标准方程;
(Ⅱ)求得切线方程,利用点到直线的距离公式可知$x_0^4=4x_0^2+4{p^2}$,将切线方程代入椭圆方程,求得丨PQ丨,分别表示出S1,S2,根据基本不等式的性质,即可求得$\frac{S_1}{S_2}$的最小值.
解答 解:(Ⅰ)设点$M({x_0},\frac{x_0^2}{2p})$,由x2=2py(p>0)得,$y=\frac{x^2}{2p}$,求导$y'=\frac{x}{p}$,
而直线MQ的斜率为1,
∴$\frac{x_0}{p}=1$且${x_0}-\frac{x_0^2}{2p}-\sqrt{2}=0$,
解得:$p=2\sqrt{2}$.
∴抛物线的标准方程:x2=4$\sqrt{2}$y;…(4分)
(Ⅱ)因为点M处的切线方程为:$y-\frac{x_0^2}{2p}=\frac{x_0}{p}(x-{x_0})$,即$2{x_0}x-2py-x_0^2=0$,
根据切线又与圆相切,得d=r,即$\frac{{|{-x_0^2}|}}{{\sqrt{4x_0^2+4{p^2}}}}=1$,化简得$x_0^4=4x_0^2+4{p^2}$,
4p2=x04-4x02>0,解得:丨x0丨>2,
由方程组$\left\{\begin{array}{l}{2{x}_{0}x-2py-{x}_{0}^{2}=0}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,解得:Q($\frac{2}{{x}_{0}}$,$\frac{4-{x}_{0}^{2}}{2p}$),
由丨PQ丨=$\sqrt{1+{k}^{2}}$丨xP-xQ丨=$\sqrt{1+\frac{{x}_{0}^{2}}{{p}^{2}}}$丨x0-$\frac{2}{{x}_{0}}$丨=$\frac{丨{x}_{0}丨}{2p}$(x02-2),
点F(0,$\frac{p}{2}$)到切线PQ的距离d=$\frac{丨-{p}^{2}-{x}_{0}^{2}丨}{\sqrt{4{x}_{0}^{2}+4{p}^{2}}}$=$\frac{1}{2}$$\sqrt{{x}_{0}^{2}+{p}^{2}}$=$\frac{{x}_{0}^{2}}{4}$,
则S1=$\frac{1}{2}$丨PQ丨•d=$\frac{丨{x}_{0}^{2}丨}{16p}$(x02-2),S1=$\frac{1}{2}$丨OF丨•丨xQ丨=$\frac{p}{2丨{x}_{0}丨}$,
∴$\frac{S_1}{S_2}$=$\frac{{x}_{0}^{4}({x}_{0}^{2}-2)}{8{p}^{2}}$=$\frac{{x}_{0}^{4}({x}_{0}^{2}-2)}{2({x}_{0}^{4}-4{x}_{0}^{2})}$=$\frac{{x}_{0}^{2}({x}_{0}^{2}-2)}{2({x}_{0}^{2}-4)}$=$\frac{{x}_{0}^{2}-4}{2}$+$\frac{4}{{x}_{0}^{2}-4}$+3≥2$\sqrt{2}$+3,
当且仅当$\frac{{x}_{0}^{2}-4}{2}$=$\frac{4}{{x}_{0}^{2}-4}$时,取“=”号,即x02=4+2$\sqrt{2}$,此时p=$\sqrt{2+2\sqrt{2}}$,
所以$\frac{S_1}{S_2}$的最小值为$3+2\sqrt{2}$.…(12分)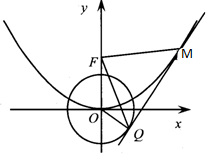
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,考查导数的几何意义,抛物线切线方程的求法,基本不等式的应用,考查计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | $±\sqrt{3}$ | C. | ±2 | D. | $±\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{5},0)$ | B. | $(\frac{2π}{5},0)$ | C. | $(\frac{3π}{5},0)$ | D. | $(\frac{4π}{5},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
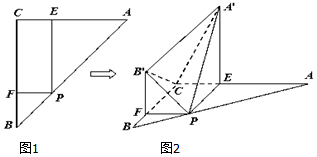 如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
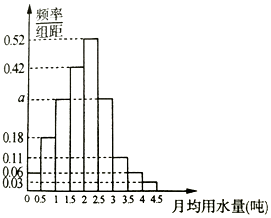 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com