
分析 (I)利用等差数列与等比数列的信托公司即可得出.
(II)l利用等差数列与等比数列的求和公式即可得出.
解答 解:(Ⅰ)设等差数列{an}的公差为d≠0,∵a2=4,且a1,a3,a9成等比数列.
即4-d,4+d,4+7d成等比数列,
所以有(4-d)(4+7d)=(4+d)2,
即d2-2d=0,d≠0.
解得d=2,
∴an=a2+(n-2)×2=4+2n-4=2n.
(Ⅱ)由(Ⅰ)知:bn=an+${2}^{{a}_{n}}$=2n+4n,
∴Tn=2(1+2+…+n)+(4+42+…+4n)
=$2×\frac{n(1+n)}{2}$+$\frac{4({4}^{n}-1)}{4-1}$
=n2+n+$\frac{{4}^{n+1}-4}{3}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 略有盈利 | B. | 无法判断盈亏情况 | ||
| C. | 没有盈也没有亏损 | D. | 略有亏损 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
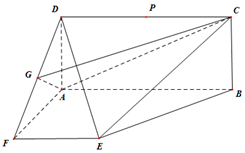 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,0) | C. | (0,1) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 互斥但不相互独立 | B. | 相互独立但不互斥 | ||
| C. | 互斥且相互独立 | D. | 既不相互独立也不互斥 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com