
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求不等式![]() 的解集;
的解集;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() (
(![]() )(若
)(若![]() 是函数
是函数![]() 的极大值或极小值,则m为函数
的极大值或极小值,则m为函数![]() 的极值点,极大值点与极小值点统称为极值点).
的极值点,极大值点与极小值点统称为极值点).
①求a的取值范围;
②证明:![]() .
.
【答案】(1)![]() .(2)①
.(2)①![]() ;②证明见解析
;②证明见解析
【解析】
(1)不等式变形为![]() ,令
,令![]() ,利用导数研究
,利用导数研究![]() 的单调性,结合
的单调性,结合![]() ,可得不等式的解集;
,可得不等式的解集;
(2)①求出导函数![]() ,再由
,再由![]() 的导数研究
的导数研究![]() 的单调性,得
的单调性,得![]() 的正负,从而得
的正负,从而得![]() 的单调性,由
的单调性,由![]() 的极小值小于0及零点存在定理可得
的极小值小于0及零点存在定理可得![]() 的范围,②由极值点定义知
的范围,②由极值点定义知![]() 是
是![]() 的极大值点,
的极大值点,![]() 是极小值点,从而有
是极小值点,从而有![]() ,
,
设![]() ,则
,则![]() 为偶函数,利用导数研究
为偶函数,利用导数研究![]() 的单调性得
的单调性得![]() ,从而可证题设结论.
,从而可证题设结论.
(1)由![]() 得
得![]()
令![]() ,∴
,∴![]() ,令
,令![]()
当![]() 时,
时,![]() ,
,![]() 递减;当
递减;当![]() 时,
时,![]() ,
,![]() 递增
递增
∴![]()
注意到![]() ,结合单调性知不等式的解集为
,结合单调性知不等式的解集为![]()
(2)![]()
![]() ,由题意知
,由题意知![]() 有
有![]() 上有两个不等的实根
上有两个不等的实根
令![]() ,令
,令![]()
当![]() 时,
时,![]() ,
,![]() 递减;当
递减;当![]() 时,
时,![]() ,
,![]() 递增,
递增,
∴![]()
要使![]() 有两个零点,则
有两个零点,则![]() ,此时注意到
,此时注意到![]()
![]() ,∴
,∴![]() 在
在![]() 和
和![]() 上各有一个零点,满足题意,故
上各有一个零点,满足题意,故![]() 的取值范围为
的取值范围为![]()
②由![]() 为
为![]() 的2个极值点,且
的2个极值点,且![]()
∴![]() 满足
满足![]() 且由①知
且由①知![]()
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
则![]() 是
是![]() 的极大值点,
的极大值点,![]() 是极小值点
是极小值点
∴![]()
设![]() ,则
,则![]() 为偶函数
为偶函数
![]() ,
,![]()
∴![]() 在
在![]() 上单调递增
上单调递增
由![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增
上单调递增
∴![]() ,
,![]()
又![]() 为偶函数,∴
为偶函数,∴![]() ,
,![]() ,∴
,∴![]()
从而![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的的菱形,
的的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(2)设点过![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且满足
上的点,且满足![]() 为等边三角形,求
为等边三角形,求![]() 边长的取值范围.
边长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
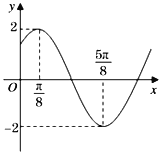
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(Ⅱ)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月![]() 时的气温,随机选取该月中的
时的气温,随机选取该月中的![]() 天,将这
天,将这![]() 天中
天中![]() 时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月
时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月![]() 时的平均气温低于乙地该月
时的平均气温低于乙地该月![]() 时的平均气温;②甲地该月
时的平均气温;②甲地该月![]() 时的平均气温高于乙地该月
时的平均气温高于乙地该月![]() 时的平均气温;③甲地该月
时的平均气温;③甲地该月![]() 时的气温的中位数小于乙地该月
时的气温的中位数小于乙地该月![]() 时的气温的中位数;④甲地该月
时的气温的中位数;④甲地该月![]() 时的气温的中位数大于乙地该月
时的气温的中位数大于乙地该月![]() 时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )
时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮).在相同的条件下,每轮甲乙两人站在同一位置上,甲先投,每人投一次篮,两人有![]() 人命中,命中者得
人命中,命中者得![]() 分,未命中者得
分,未命中者得![]() 分;两人都命中或都未命中,两人均得
分;两人都命中或都未命中,两人均得![]() 分.设甲每次投篮命中的概率为
分.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.
,且各次投篮互不影响.
(1)经过![]() 轮投篮,记甲的得分为
轮投篮,记甲的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
(2)若经过![]() 轮投篮,用
轮投篮,用![]() 表示第
表示第![]() 轮投篮后,甲的累计得分低于乙的累计得分的概率.
轮投篮后,甲的累计得分低于乙的累计得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机模拟计算可得
,经过计算机模拟计算可得![]() ,请根据①中
,请根据①中![]() 值求出
值求出![]() 的值,并由此求出数列
的值,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com