已知实数x、y满足x2+y2≤1,则|x+y|+|y+1|+|2y-x-4|的取值范围是 .
【答案】
分析:令x=cosθ,y=sinθ,θ∈[-π,π],z=|x+y|+|y+1|+|2y-x-4|,化简可得z=|
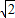
sin(θ+
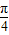
)|+5+cosθ-sinθ.
当θ∈[-
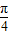
,
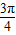
]时,化简z,并求出其范围,当θ∈[-π,-
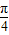
]∪[
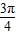
,π]时,化简z,并求出其范围,将这两个范围取并集即为所求.
解答:解:令x=cosθ,y=sinθ,θ∈[-π,π].
设 z=|x+y|+|y+1|+|2y-x-4|=|cosθ+sinθ|+|sinθ+1|+|2sinθ-cosθ-4|=|cosθ+sinθ|+sinθ+1+(-2sinθ+cosθ+4)
=|
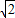
sin(θ+
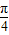
)|+5+cosθ-sinθ.
当θ∈[-
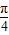
,
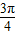
]时,cosθ+sinθ=
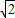
sin(θ+
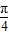
)≥0,z=cosθ+sinθ+5+cosθ-sinθ=5+2cosθ,
5-
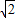
≤z≤7.
当θ∈[-π,-
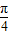
]∪[
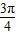
,π]时,cosθ+sinθ=
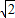
sin(θ+
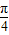
)≤0,z=-(cosθ+sinθ)+5+cosθ-sinθ=5-2sinθ,
5-
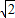
≤z≤7.
综上,5-
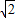
≤z≤7,
故答案为:
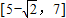
.
点评:本题主要考查带绝对值的函数,三角恒等代换,正弦函数的定义域和值域,体现了分类讨论的数学思想,属于中档题.

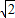 sin(θ+
sin(θ+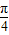 )|+5+cosθ-sinθ.
)|+5+cosθ-sinθ.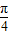 ,
,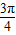 ]时,化简z,并求出其范围,当θ∈[-π,-
]时,化简z,并求出其范围,当θ∈[-π,-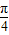 ]∪[
]∪[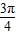 ,π]时,化简z,并求出其范围,将这两个范围取并集即为所求.
,π]时,化简z,并求出其范围,将这两个范围取并集即为所求.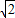 sin(θ+
sin(θ+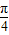 )|+5+cosθ-sinθ.
)|+5+cosθ-sinθ.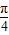 ,
,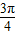 ]时,cosθ+sinθ=
]时,cosθ+sinθ=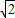 sin(θ+
sin(θ+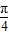 )≥0,z=cosθ+sinθ+5+cosθ-sinθ=5+2cosθ,
)≥0,z=cosθ+sinθ+5+cosθ-sinθ=5+2cosθ,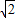 ≤z≤7.
≤z≤7.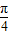 ]∪[
]∪[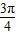 ,π]时,cosθ+sinθ=
,π]时,cosθ+sinθ=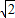 sin(θ+
sin(θ+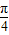 )≤0,z=-(cosθ+sinθ)+5+cosθ-sinθ=5-2sinθ,
)≤0,z=-(cosθ+sinθ)+5+cosθ-sinθ=5-2sinθ,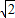 ≤z≤7.
≤z≤7.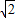 ≤z≤7,
≤z≤7,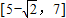 .
.
