
如图,直四棱柱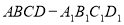 的底面
的底面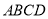 是平行四边形,
是平行四边形,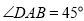 ,
, 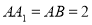 ,
,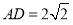 ,点
,点 是
是  的中点,点
的中点,点 在
在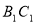 且
且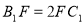 .
.

(Ⅰ)证明: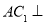 平面
平面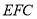 ;
;
(Ⅱ)求锐二面角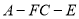 平面角的余弦值.
平面角的余弦值.
(1)见解析;(2)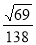 .
.
【解析】
试题分析:(1)利用已知的垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明证线面垂直,只需要证明直线的方向向量垂直与平面的法向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(Ⅰ)以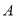 为坐标原点,射线
为坐标原点,射线 为
为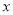 轴的正半轴,建立如图所示空间直角坐标系
轴的正半轴,建立如图所示空间直角坐标系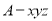 .则依题意,可得以下各点的坐标分别为
.则依题意,可得以下各点的坐标分别为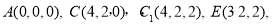
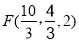 .
.

∴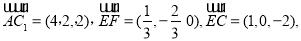
∴ 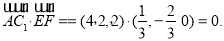
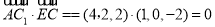
∴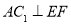 ,
,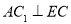 .又
.又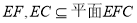
∴ 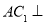 平面
平面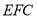 .
.
(Ⅱ)设向量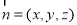 是平面
是平面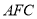 的法向量,则
的法向量,则 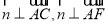 ,
,
而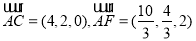 ∴
∴ 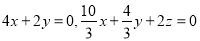 ,
,
令 得
得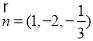 .
.
又∵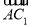 是平面
是平面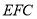 的法向量,
的法向量,
∴ 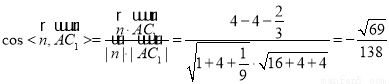 .
.
所以锐二面角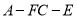 平面角的余弦值为
平面角的余弦值为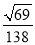 .
.
考点:利用空间向量证明线面垂直和求夹角 .


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:2015届山东省高二下学期期中质量检测试卷(解析版) 题型:解答题
已知 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 .
.
(1)若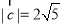 ,且
,且 //
// ,求
,求 的坐标;
的坐标;
(2) 若| |=
|= 且
且 +2
+2 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省文登市高二下学期期末理科数学试卷(解析版) 题型:选择题
有 个座位连成一排,安排
个座位连成一排,安排 个人就座,恰有两个空位相邻的不同坐法有
个人就座,恰有两个空位相邻的不同坐法有
A. 种 B.
种 B. 种 C.
种 C. 种 D.
种 D. 种
种
查看答案和解析>>
科目:高中数学 来源:2015届山东省乳山市高二下学期中考试文科数学试卷(解析版) 题型:填空题
对大于或等于2的自然数m的n次方幂有如下分解式: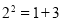 ,
,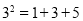 ,
,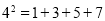 ,
,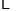 ;
;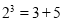 ,
,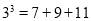 ,
,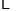 ;
;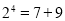 ,
,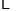 ;按此规律,
;按此规律,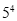 的分解式中的第4个数为 ____ .
的分解式中的第4个数为 ____ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com