
分析 (Ⅰ)求出X=3时的概率即可;
(Ⅱ)由题意可知X可取的值为1,2,3,4,5,分别求出相对应的概率,求出分布列,进而求出其期望值.
解答 解:(Ⅰ)由题意得$P(X=3)=C_4^2{(\frac{1}{3})^2}(\frac{2}{3})=\frac{8}{27}$;
(Ⅱ)由题意可知X可取的值为1,2,3,4,5,
它们的概率为:$P(X=1)=C_4^0{(\frac{1}{3})^4}=\frac{1}{81}$,$P(X=2)=C_4^1(\frac{2}{3}){(\frac{1}{3})^3}=\frac{8}{81}$,
$P(X=3)=C_4^2{(\frac{2}{3})^2}{(\frac{1}{3})^2}=\frac{24}{81}$,$P(X=4)=C_4^3{(\frac{2}{3})^3}(\frac{1}{3})=\frac{32}{81}$,
$P(X=5)=C_4^4{(\frac{2}{3})^4}=\frac{16}{81}$,
故其分布列为
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{81}$ | $\frac{8}{81}$ | $\frac{24}{81}$ | $\frac{32}{81}$ | $\frac{16}{81}$ |
点评 本题考察了离散型随机变量,考察分布列及方差,是一道中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:选择题
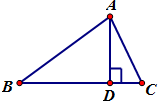 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
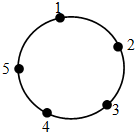 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{4}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com