
ЁОЬтФПЁПФГЛњЙЙЮЊСЫбаОПШЫЕФНХЕФДѓаЁгыЩэИпжЎМфЕФЙиЯЕЃЌЫцЛњВтСПСЫ20ШЫЃЌЕУЕНШчЯТЪ§ОнЃК


(1) ШєЁАЩэИпДѓгк175РхУзЁБЕФЮЊЁАИпИіЁБЃЌЁАЩэИпаЁгкЕШгк175РхУзЁБЕФЮЊЁАЗЧИпИіЁБЃЛЁАНХГЄДѓгк42ТыЁБЕФЮЊЁАДѓНХЁБЃЌЁАНХГЄаЁгкЕШгк42ТыЁБЕФЮЊЁАЗЧДѓНХЁБЃЌЧыИљОнЩЯБэЪ§ОнЭъГЩЯТУцЕФ2ЁС2СаСЊБэ.

(2)ИљОн(1)жаЕФ2ЁС2СаСЊБэЃЌдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.01ЕФЧАЬсЯТЃЌФмЗёШЯЮЊНХЕФДѓаЁгыЩэИпжЎМфгаЙиЯЕЃП
![]() ЃЌ
ЃЌ
![]()

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіжБНЧШ§НЧаЮЕФШ§ИіЖЅЕуЗжБ№дкЕзУцРтГЄЮЊ2ЕФе§Ш§РтжљЕФВрРтЩЯЃЌдђИУжБНЧШ§НЧаЮаББпЕФзюаЁжЕЮЊ__________ЃЎ
ЁОД№АИЁП![]()
ЁОНтЮіЁП ШчЭМЃЌВЛЗСЩш
ШчЭМЃЌВЛЗСЩш![]() дк
дк![]() ДІЃЌ
ДІЃЌ ![]() ЃЌ
ЃЌ
дђга![]() гЩ
гЩ![]()
![]() ИУжБНЧШ§НЧаЮаББп
ИУжБНЧШ§НЧаЮаББп![]()
ЙЪД№АИЮЊ![]() .
.
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
16
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃН![]() ЃЌgЃЈxЃЉЃН
ЃЌgЃЈxЃЉЃН![]() ЃЌШєКЏЪ§yЃНfЃЈgЃЈxЃЉЃЉЃЋaгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЈЦфжаx1ЃМx2ЃМx3ЃЉЃЌдђ2gЃЈx1ЃЉЃЋgЃЈx2ЃЉЃЋgЃЈx3ЃЉЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ЃЌШєКЏЪ§yЃНfЃЈgЃЈxЃЉЃЉЃЋaгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЈЦфжаx1ЃМx2ЃМx3ЃЉЃЌдђ2gЃЈx1ЃЉЃЋgЃЈx2ЃЉЃЋgЃЈx3ЃЉЕФШЁжЕЗЖЮЇЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮПМЪдЙВга10ЕРбЁдёЬтЃЌУПЕРбЁдёЬтЖМга4ИібЁЯюЃЌЦфжагаЧвжЛгавЛИіЪЧе§ШЗЕФЃЎЦРЗжБъзМЙцЖЈЃКЁАУПЬтжЛбЁвЛИібЁЯюЃЌД№ЖдЕУ5ЗжЃЌВЛД№ЛђД№ДэЕУСуЗжЁБЃЎФГПМЩњвбШЗЖЈга7ЕРЬтЕФД№АИЪЧе§ШЗЕФЃЌЦфгрЬтжаЃКгавЛЕРЬтЖМПЩХаЖЯСНИібЁЯюЪЧДэЮѓЕФЃЌгавЛЕРЬтПЩвдХаЖЯвЛИібЁЯюЪЧДэЮѓЕФЃЌЛЙгавЛЕРЬтвђВЛРэНтЬтвтжЛКУТвВТЃЎЪдЧѓГіИУПМЩњЃК
ЃЈЂёЃЉЕУ50ЗжЕФИХТЪЃЛ
ЃЈЂђЃЉЫљЕУЗжЪ§![]() ЕФЪ§бЇЦкЭћЃЈгУаЁЪ§БэЪОЃЌОЋШЗЕН0.01k^s*5#uЃЉ
ЕФЪ§бЇЦкЭћЃЈгУаЁЪ§БэЪОЃЌОЋШЗЕН0.01k^s*5#uЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= 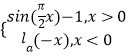 ЃЈaЃО0ЃЌЧвaЁй1ЃЉЕФЭМЯѓЩЯЙигкyжсЖдГЦЕФЕужСЩйга5ЖдЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЃЈaЃО0ЃЌЧвaЁй1ЃЉЕФЭМЯѓЩЯЙигкyжсЖдГЦЕФЕужСЩйга5ЖдЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈ0ЃЌ ![]() ЃЉ
ЃЉ
B.ЃЈ ![]() ЃЌ1ЃЉ
ЃЌ1ЃЉ
C.ЃЈ ![]() ЃЌ1ЃЉ
ЃЌ1ЃЉ
D.ЃЈ0ЃЌ ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтИпжаЩњзїЮФГЩМЈгыПЮЭтдФЖССПжЎМфЕФЙиЯЕЃЌФГбаОПЛњЙЙЫцЛњГщШЁСЫ60УћИпжаЩњЃЌЭЈЙ§ЮЪОэЕїВщЃЌЕУЕНвдЯТЪ§ОнЃК
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

гЩвдЩЯЪ§ОнЃЌМЦЫуЕУЕНK2ЕФЙлВтжЕkЁж9.643ЃЌИљОнСйНчжЕБэЃЌвдЯТЫЕЗЈе§ШЗЕФЪЧ(ЁЁЁЁ)
A. УЛгаГфзуЕФРэгЩШЯЮЊПЮЭтдФЖССПДѓгызїЮФГЩМЈгХаугаЙи
B. га0.5%ЕФАбЮеШЯЮЊПЮЭтдФЖССПДѓгызїЮФГЩМЈгХаугаЙи
C. га99.9%ЕФАбЮеШЯЮЊПЮЭтдФЖССПДѓгызїЮФГЩМЈгХаугаЙи
D. га99.5%ЕФАбЮеШЯЮЊПЮЭтдФЖССПДѓгызїЮФГЩМЈгХаугаЙи
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвбжЊдВCЕФдВаФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌАыОЖЮЊ ![]() ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК
ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК ![]() ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓдВCКЭжБЯпlЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЕуPЕФМЋзјБъЮЊЃЈ1ЃЌ ![]() ЃЉЃЌжБЯпlгыдВCЯрНЛгкAЃЌBЃЌЧѓ|PA|+|PB|ЕФжЕЃЎ
ЃЉЃЌжБЯпlгыдВCЯрНЛгкAЃЌBЃЌЧѓ|PA|+|PB|ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=2cos2Іиx+2 ![]() sinІиxcosІиxЉ1ЃЌЧвfЃЈxЃЉЕФжмЦкЮЊ2ЃЎ
sinІиxcosІиxЉ1ЃЌЧвfЃЈxЃЉЕФжмЦкЮЊ2ЃЎ
ЃЈЂёЃЉЕБ ![]() ЪБЃЌЧѓfЃЈxЃЉЕФзюжЕЃЛ
ЪБЃЌЧѓfЃЈxЃЉЕФзюжЕЃЛ
ЃЈЂђЃЉШє ![]() ЃЌЧѓ
ЃЌЧѓ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЭјИёжНЩЯаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌДжЯпЛГіЕФЪЧвЛе§ЗНЬхБЛНиШЅвЛВПЗжКѓЫљЕУМИКЮЬхЕФШ§ЪгЭМЃЌдђИУМИКЮЬхЕФБэУцЛ§ЮЊЃЈ ЃЉ 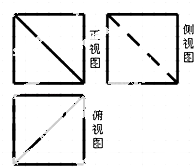
A.54
B.162
C.54+18 ![]()
D.162+18 ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗНЯђЯђСПЮЊv=ЃЈ1ЃЌ ![]() ЃЉЕФжБЯпlЙ§ЕуЃЈ0ЃЌЉ2
ЃЉЕФжБЯпlЙ§ЕуЃЈ0ЃЌЉ2 ![]() ЃЉКЭЭждВCЃК
ЃЉКЭЭждВCЃК ![]() =1ЃЈaЃОbЃО0ЃЉЕФНЙЕуЃЌЧвЭждВCЕФжааФЙигкжБЯпlЕФЖдГЦЕудкЭждВCЕФгвзМЯпЩЯЃЎ
=1ЃЈaЃОbЃО0ЃЉЕФНЙЕуЃЌЧвЭждВCЕФжааФЙигкжБЯпlЕФЖдГЦЕудкЭждВCЕФгвзМЯпЩЯЃЎ
ЃЈЂёЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈЂђЃЉЪЧЗёДцдкЙ§ЕуEЃЈЉ2ЃЌ0ЃЉЕФжБЯпmНЛЭждВCгкЕуMЁЂNЃЌТњзу ![]() =
= ![]() ЃЎcotЁЯMONЁй0ЃЈOЮЊдЕуЃЉЃЎШєДцдкЃЌЧѓжБЯпmЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЎcotЁЯMONЁй0ЃЈOЮЊдЕуЃЉЃЎШєДцдкЃЌЧѓжБЯпmЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com