练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在锐角△ABC中，内角A、B、C的对边分别为a、b、c，且2asin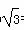B＝b.

    (1) 求角A的大小；

    (2) 若a＝6，b＋c＝8，求△ABC的面积．


    解：(1) 由2asinB＝b及正弦定理＝，得sinA＝.因为A是锐角，所以A＝.

    (2) 由余弦定理a2＝b2＋c2－2bccosA，得b2＋c2－bc＝36.又b＋c＝8，所以bc＝.

    由三角形面积公式S＝bcsinA，得△ABC的面积为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     某科研单位欲拿出一定的经费奖励科研人员，第1名得全部资金的一半多一万元，第2名得剩下的一半多一万元，以名次类推都得到剩下的一半多一万元，到第10名恰好资金分完，则此科研单位共拿出________万元资金进行奖励．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，若a＝1，b＝2，cosC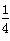＝.求：

    (1) △ABC的周长；

    (2) cos(A－C)的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v海里/时的航行速度匀速行驶，经过t小时与轮船相遇．

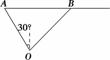
    (1) 若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

    (2) 假设小艇的最高航行速度只能达到30海里/时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，AC＝，BC＝2，B＝60°，则边BC上的高为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝cos的最小正周期为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，a＝3，b＝2，∠B＝2∠A.

    (1) 求cosA的值；

    (2) 求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知sin2α＝，则cos2＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若经过点P(1－a，1＋a)和Q(3，2a)的直线的倾斜角为锐角，则实数a的取值范围是________．

    查看答案和解析>>

    同步练习册答案