
���� �����������ַ��̻���������������C1����ͨ����������C2��ֱ�����귽�̣�
����������C1������C2�ཻ��A��B���㣬���Բ�ĵ�ֱ�ߵľ��룬������|AB|��ֵ��
��� �⣺������$\left\{\begin{array}{l}x=cos��\\ y=1+sin��\end{array}\right.⇒\left\{\begin{array}{l}x=cos��\\ y-1=sin��\end{array}\right.⇒{x^2}+{��y-1��^2}=1$��3��
��$��sin����-\frac{��}{4}��=\sqrt{2}⇒\frac{{\sqrt{2}}}{2}��sin��-\frac{{\sqrt{2}}}{2}��cos��=\sqrt{2}⇒y-x=2$
��C2��x-y+2=0����6��
����ֱ��x-y+2=0��Բx2+��y-1��2=1�ཻ��A��B���㣬
��x2+��y-1��2=1��Բ�ģ�0��1����Ϊ�뾶Ϊ1��
��Բ�ĵ�ֱ�ߵľ���$d=\frac{|0-1+2|}{{\sqrt{{1^2}+{{��-1��}^2}}}}=\frac{{\sqrt{2}}}{2}$��
��$|AB|=2\sqrt{{1^2}-{{��\frac{{\sqrt{2}}}{2}��}^2}}=\sqrt{2}$����10�֣�
���� ���⿼�����ַ��̵Ļ�����������ֱ����Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
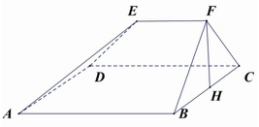 ��ͼ��������ABCDEF�У���֪ABCD�DZ߳�Ϊ3�������Σ���FBC��BC���ϵĸ�ΪFH��EF��FH��EF��AB��
��ͼ��������ABCDEF�У���֪ABCD�DZ߳�Ϊ3�������Σ���FBC��BC���ϵĸ�ΪFH��EF��FH��EF��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-ln3��x��ln3} | B�� | {x|x��-ln3����x��ln3} | ||
| C�� | {x|-ln3��x��0����x��ln3} | D�� | {x|x��-ln3����0��x��ln3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
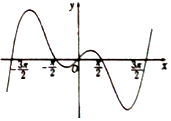
| A�� | f��x��=x+sinx | B�� | f��x��=$\frac{cosx}{x}$ | C�� | f��x��=x��x-$\frac{��}{2}$����x-$\frac{3��}{2}$�� | D�� | f��x��=xcosx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com