
(本小题满分13分)
在数列{an}中,a1=1,an=n2[1+ +
+ +…+
+…+ ] (n≥2,n∈N)
] (n≥2,n∈N)
(1)当n≥2时,求证: =
=
(2)求证:(1+ )(1+
)(1+ )…(1+
)…(1+ )<4
)<4
(1)利用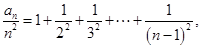
得到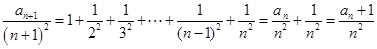 。
。
(2)当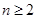 时,
时,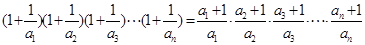
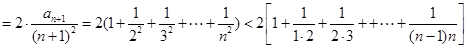
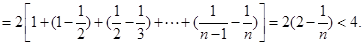
验证,当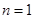 时,
时,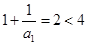 ,综上所述,对任意
,综上所述,对任意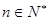 ,不等式都成立.
,不等式都成立.
解析试题分析:(1)当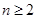 时,
时, 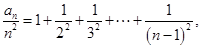 ……………………1分
……………………1分
所以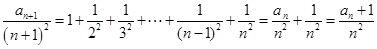 …………………4分
…………………4分
故
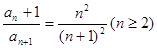 …………………………………………………………5分
…………………………………………………………5分
(2)当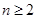 时,
时,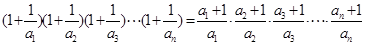 ……6分
……6分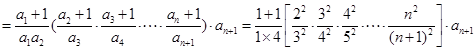 ……8分
……8分 ……10分
……10分 ………………………11分
………………………11分
当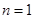 时,
时,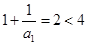 ……………………………………………………………12分
……………………………………………………………12分
综上所述,对任意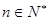 ,不等式都成立.……………………………………13分
,不等式都成立.……………………………………13分
考点:本题主要考查数列“裂项相消法”求和,“放缩法”证明不等式。
点评:中档题,涉及数列的不等式证明问题,往往需要先求和、再证明。本题(2)利用“裂项相消法”求得“数列的和”,利用放缩法,达到证明目的。易错忽视n=1的验证。


科目:高中数学 来源: 题型:解答题
已知数列{an}是首项a1=4,公比q≠1的等比数列,Sn是其前n项和,且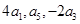 成等差数列.
成等差数列.
(1)求公比q的值;
(2)求Tn=a2+a4+a6+…+a2n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数列{an}(n∈N*)中,已知a1=1,a2k=-ak,a2k-1=(-1)k+1ak,k∈N*. 记数列{an}的前n项和为Sn.
(1)求S5,S7的值;
(2)求证:对任意n∈N*,Sn≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知数列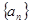 满足
满足 .
.
(1)设 ,证明:数列
,证明:数列 为等差数列,并求数列
为等差数列,并求数列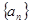 的通项公式;
的通项公式;
(2)求数列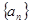 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知二次函数 同时满足:①不等式
同时满足:①不等式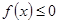 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在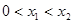 ,使得不等式
,使得不等式 成立.
成立.
设数列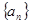 的前
的前 项和
项和 ,
,
(1)求数列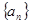 的通项公式;
的通项公式;
(2)数列 中,令
中,令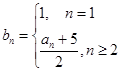 ,
,
 ,求
,求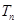 ;
;
(3)设各项均不为零的数列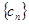 中,所有满足
中,所有满足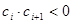 的正整数
的正整数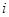 的个数称为这个数列
的个数称为这个数列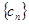 的变号数。令
的变号数。令 (
( 为正整数),求数列
为正整数),求数列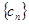 的变号数.
的变号数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com