
| A. | $-\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{3}$ | D. | $\frac{π}{3}$ |
分析 函数f(x)=$2sin(\frac{1}{2}x+θ-\frac{π}{3})$,由于函数f(x)的图象关于y轴对称,当x=0时,$sin(θ-\frac{π}{3})$=±1,又|θ|<$\frac{π}{2}}$,解出即可.
解答 解:函数f(x)=sin(${\frac{1}{2}$x+θ)-$\sqrt{3}$cos(${\frac{1}{2}$x+θ)=$2sin(\frac{1}{2}x+θ-\frac{π}{3})$,
∵函数f(x)的图象关于y轴对称,
∴当x=0时,$sin(θ-\frac{π}{3})$=±1,
又|θ|<$\frac{π}{2}}$,
解得$θ=-\frac{π}{6}$,
故选:A.
点评 本题考查了和差公式、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∨q | C. | ¬p∧q | D. | ¬p∨¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
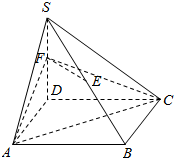 如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证:
如图,四棱锥S-ABCD中,侧棱SD垂直于正方形ABCD所在的平面,E、F分别是SB、SD的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-1,1)使得cosx<$\frac{1}{2}$ | |
| B. | “-3<m<0”是“函数f(x)=x+log2x+m在区间($\frac{1}{2}$,2)上有零点”的必要不充分条件 | |
| C. | x=$\frac{π}{6}$是曲线f(x)=$\sqrt{3}$sin2x+cos2x的一条对称轴 | |
| D. | 若x∈(0,2),则在曲线f(x)=ex(x-2)上任意一点处的切线的斜率不小于-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com