
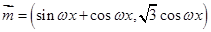 ,
,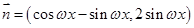 ,其中
,其中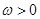 ,若函数
,若函数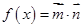 ,且函数
,且函数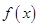 的图象与直线y=2两相邻公共点间的距离为
的图象与直线y=2两相邻公共点间的距离为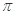 .
.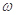 的值;
的值;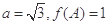 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.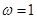 ;(2)
;(2)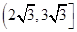 .
.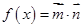 ,结合二倍角公式以及和角公式化简,求得
,结合二倍角公式以及和角公式化简,求得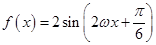 ,函数最大值是
,函数最大值是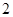 ,那么函数
,那么函数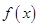 的图像与直线
的图像与直线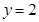 两相邻公共点间的距离
两相邻公共点间的距离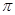 正好是一个周期,然后根据
正好是一个周期,然后根据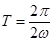 求解
求解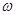 的值;(2)先将
的值;(2)先将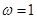 代入函数
代入函数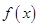 的解析式得到:
的解析式得到: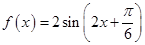 ,由已知条件
,由已知条件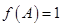 以及
以及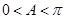 ,结合三角函数的图像与性质可以解得
,结合三角函数的图像与性质可以解得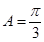 ,所以
,所以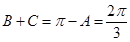 ,由正弦定理得
,由正弦定理得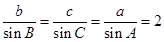 ,那么
,那么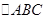 的周长可以表示为:
的周长可以表示为: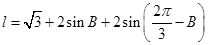 ,由差角公式以及和角公式将此式化简整理得,
,由差角公式以及和角公式将此式化简整理得,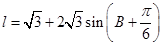 ,结合角
,结合角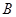 的取值以及三角函数的图像与性质可得
的取值以及三角函数的图像与性质可得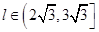 .
.

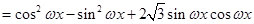
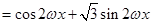
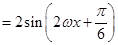 , 3分
, 3分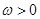 ,
,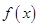 的周期
的周期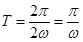 ,
,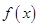 的图象与直线
的图象与直线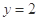 两相邻公共点间的距离为
两相邻公共点间的距离为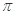 .
.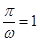 ,解得
,解得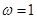 . 4分
. 4分 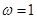 ,
,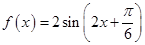 ,
,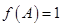 ,∴
,∴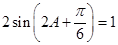 ,即
,即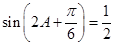 ,
,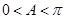 ,∴
,∴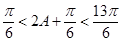 ,
,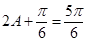 ,解得
,解得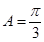 . 7分
. 7分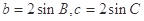 ,
,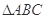 周长为:
周长为: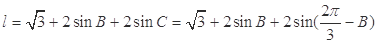
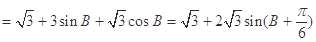 , 10分
, 10分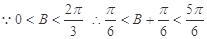 ,
,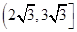 . 12分
. 12分

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:填空题
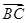 =λ
=λ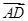 (λ∈R),|
(λ∈R),|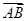 |=|
|=|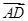 |=2,|
|=2,|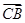 -
-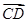 |=2
|=2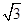 ,且△BCD是以BC为斜边的直角三角形,则
,且△BCD是以BC为斜边的直角三角形,则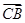 ·
·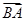 的值为__________.
的值为__________.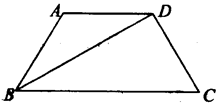
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com