
已知直线l: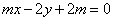 (m
(m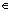 R)和椭圆C:
R)和椭圆C: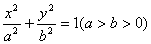 , 椭圆C的离心率为
, 椭圆C的离心率为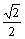 ,连接椭圆的四个顶点形成四边形的面积为2
,连接椭圆的四个顶点形成四边形的面积为2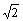 .
.
⑴求椭圆C的方程;
⑵直线l/与椭圆C有两个不同的交点,求实数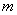 的取值范围;
的取值范围;
⑶当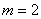 时,设直线l与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值。
时,设直线l与y轴的交点为P,M为椭圆C上的动点,求线段PM长度的最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com