
【题目】定义区间![]() 的长度均为
的长度均为![]() ,其中
,其中![]()
(1)若函数![]() 的定义域为
的定义域为![]() 值域为
值域为![]() 写出区间长度
写出区间长度![]() 的最大值;
的最大值;
(2)若关于![]() 的不等式组
的不等式组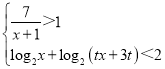 的解集构成的各区间长度和为6,求实数
的解集构成的各区间长度和为6,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 求证:关于
求证:关于![]() 的不等式
的不等式![]() 的解集构成的各区间的长度和为定值.
的解集构成的各区间的长度和为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)定值为
;(3)定值为![]() ,证明见解析.
,证明见解析.
【解析】
(1)令![]() 求得函数的零点,令
求得函数的零点,令![]() ,求得定义域区间长度最大时
,求得定义域区间长度最大时![]() 的值.
的值.
(2)先求得不等式![]() 的解集
的解集![]() ,设不等式
,设不等式![]() 的解集为
的解集为![]() ,根据
,根据![]() 的长度为
的长度为![]() 列不等式组,由此求得
列不等式组,由此求得![]() 的取值范围.
的取值范围.
(3)将原不等式![]() 转化为分式不等式的形式,结合高次不等式的解法,求得不等式的解集,进而求得不等式解集构成的各区间的长度和为定值
转化为分式不等式的形式,结合高次不等式的解法,求得不等式的解集,进而求得不等式解集构成的各区间的长度和为定值![]() .
.
(1)令![]() ,解得
,解得![]() ,此时
,此时![]() 为函数的最小值.令
为函数的最小值.令![]() ,解得
,解得![]() ,
,![]() .故定义域区间长度最大时
.故定义域区间长度最大时![]() ,故区间
,故区间![]() 的长度为
的长度为![]() .
.
(2)由![]() 得
得![]() ,解得
,解得![]() ,记
,记![]() .设不等式
.设不等式![]() 的解集为
的解集为![]() ,不等式组
,不等式组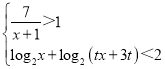 的解集为
的解集为![]() .
.
设不等式![]() 等价于
等价于 ,所以
,所以![]() ,
,![]() ,由于不等式组的解集的个区间长度和为
,由于不等式组的解集的个区间长度和为![]() ,所以不等式组
,所以不等式组 ,当
,当![]() 是恒成立.
是恒成立.
当![]() 时,不等式
时,不等式![]() 恒成立,得
恒成立,得![]() .
.
当![]() 时,不等式
时,不等式![]() 恒成立,分离常数得
恒成立,分离常数得![]() 恒成立. 当
恒成立. 当![]() 时,
时,![]() 为单调递增函数,所以
为单调递增函数,所以![]() ,所以
,所以![]() ,所以实数
,所以实数![]() .
.
(3)原不等式![]() 可化为
可化为
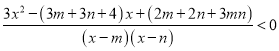 ①.
①.
令![]() ,其判别式
,其判别式![]()
![]() ,所以
,所以![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,设
,设![]() ,则
,则![]() ,根据求根公式可求得
,根据求根公式可求得![]() .而
.而![]() ,
,![]() .
.
i)当![]() 时,不等式①等价于
时,不等式①等价于![]() ,解得
,解得![]() ,即不等式①的解集为
,即不等式①的解集为![]() ,区间长度为
,区间长度为![]() .
.
ii)当![]() 时,不妨设
时,不妨设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .此时不等式①即
.此时不等式①即![]() ,解得
,解得![]() 或
或![]() ,即不等式①的解集为
,即不等式①的解集为![]() ,区间的长度为
,区间的长度为![]()
![]() .
.
综上所述,关于![]() 的不等式
的不等式![]() 的解集构成的各区间的长度和为定值
的解集构成的各区间的长度和为定值![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,![]() 、
、![]() 为左、右焦点,焦距是实轴长的
为左、右焦点,焦距是实轴长的![]() 倍,双曲线过点
倍,双曲线过点![]() .
.
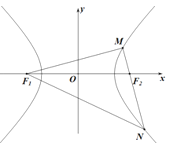
(1)求双曲线的标准方程;
(2)若点![]() 在双曲线上,求证:点
在双曲线上,求证:点![]() 在以
在以![]() 为直径的圆上;
为直径的圆上;
(3)在(2)的条件下,若直线![]() 交双曲线于另一点
交双曲线于另一点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低空气污染,提高环境质量,政府决定对汽车尾气进行整治.某厂家生产甲、乙两种不同型号的汽车尾气净化器,为保证净化器的质量,分别从甲、乙两种型号的净化器中随机抽取100件作为样本进行产品性能质量评估,评估综合得分![]() 都在区间
都在区间![]() .已知评估综合得分与产品等级如下表:
.已知评估综合得分与产品等级如下表:

根据评估综合得分,统计整理得到了甲型号的样本频数分布表和乙型号的样本频率分布直方图(图表如下).


甲型 乙型
(Ⅰ)从厂家生产的乙型净化器中随机抽取一件,估计这件产品为二级品的概率;
(Ⅱ)从厂家生产的乙型净化器中随机抽取3件,设随机变量![]() 为其中二级品的个数,求
为其中二级品的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两种型号汽车尾气净化器的优劣情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 为公比不为1的等比数列,求q的值,使数列
为公比不为1的等比数列,求q的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() 且
且![]() ,数列
,数列![]() 有最大值M与最小值
有最大值M与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为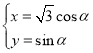 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P—ABCD中,![]() PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.
PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.

(1)求证:MN//平面PAD;
(2)求二面角B—AM—C的大小;
(3)在BC上是否存在点E,使得EN⊥平面AMV?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.命题“若![]() 则
则![]() ”的逆否命题为真
”的逆否命题为真
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.若命题p为真命题,命题q为假命题,则命题“![]() ”为真命题
”为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com