
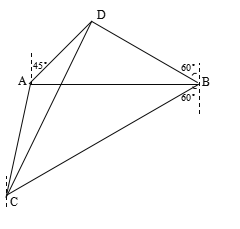
【题目】如图,A、B是海面上位于东西方向相距![]() 海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号.位于B点南偏西60°且与B相距20
海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号.位于B点南偏西60°且与B相距20![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时。求救援船直线到达D的时间和航行方向.
海里的C点的救援船立即前往营救,其航行速度为30海里/小时。求救援船直线到达D的时间和航行方向.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随机抽取100名学生,测得他们的身高(单位: ![]() ),按照区间
),按照区间![]() ,
,
![]() 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).

(1)求频率分布直方图中![]() 的值及身高在
的值及身高在![]() 以上的学生人数;
以上的学生人数;
(2)将身高在![]() 区间内的学生依次记为
区间内的学生依次记为![]() 三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
(3)在(2)的条件下,要从6名学生中抽取2人.用列举法计算![]() 组中至少有1人被抽中的概率.
组中至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
:  (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了活跃元旦晚会气氛,主持人请12位同学做一个游戏,第一轮游戏中,主持人将标有数字1到12的十二张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字7到12的卡片的同学留下,其余的淘汰;第二轮将标有数字1到6的六张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字4到6的卡片的同学留下,其余的淘汰;第三轮将标有数字1,2,3的三张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字2,3的卡片的同学留下,其余的淘汰;第四轮用同样的办法淘汰一位同学,最后留下的这位同学获得一个奖品.已知同学甲参加了该游戏.
(1)求甲获得奖品的概率;
(2)设![]() 为甲参加游戏的轮数,求
为甲参加游戏的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货商场举行年终庆典,推出以下两种优惠方案:
方案一:单笔消费每满200元立减50元,可累计;
方案二:单笔消费满200元可参与一次抽奖活动,抽奖规则如下:从装有6个小球(其中3个红球3个白球,它们除颜色外完全相同)的盒子中随机摸出3个小球,若摸到3个红球则按原价的5折付款,若摸到2个红球则按原价的7折付款,若摸到1个红球则按原价的8折付款,若未摸到红球按原价的9折付款。
单笔消费不低于200元的顾客可从中任选一种优惠方案。
(I)某顾客购买一件300元的商品,若他选择优惠方案二,求该顾客最好终支付金额不超过250元的概率。
(II)若某顾客的购物金额为210元,请用所学概率知识分析他选择哪一种优惠方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com