
分析 (1)直接利用扇形的弧长、面积公式计算.
(2)设扇形的半径为r,弧长为l,利用周长关系,表示出扇形的面积,利用二次函数求出面积的最大值,以及圆心角的大小.
解答 解:(1)根据题意得:α=60°=$\frac{π}{3}$,l=αR=$\frac{10π}{3}$cm,
S扇形=$\frac{1}{2}lR$=$\frac{1}{2}×\frac{10π}{3}×10$=$\frac{50}{3}$(cm2).
(2)设扇形的半径为r,弧长为l,则
l+2r=12,即l=12-2r(0<r<4).
扇形的面积S=$\frac{1}{2}$lr,将上式代入,
得S=$\frac{1}{2}$(12-2r)r=-r2+6r=-(r-3)2+9,
∴当且仅当r=3时,S有最大值9,
此时l=6,α=2rad.
∴当α=2rad时,扇形的面积取最大值,最大值为9cm2.
点评 本题考查了扇形面积的计算,考查扇形的周长,半径圆心角,面积之间的关系,考查计算能力.


科目:高中数学 来源: 题型:解答题
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都是奇数 | B. | 假设a,b,c至少有两个是奇数 | ||
| C. | 假设a,b,c至多有一个是奇数 | D. | 假设a,b,c不都是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题:
已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题:| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对嘉积中学的看法 | 非常好,嘉积中学奠定了 我一生成长的起点 | 很好,我的中学很快乐很充实 |
| A班人数比例 | $\frac{1}{2}$ | $\frac{1}{2}$ |
| B班人数比例 | $\frac{2}{3}$ | $\frac{1}{3}$ |
| C班人数比例 | $\frac{3}{4}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
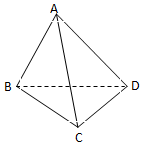 如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.
如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
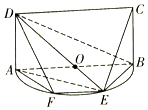 如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.
如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com