
分析 (1)化简函数f(x)的解析式,分类讨论求得y=f(x)的最小值;
(2)由条件利用绝对值的意义,求得不等式|f(x)-6|≤1的解集.
解答 解:(1)f(x)=|x-1|+|2x+4|=$\left\{\begin{array}{l}{-3x-3,x≤-2}\\{x+5,-2<x≤1}\\{3x+3,x>1}\end{array}\right.$,
所以:当x≤-2时,y∈[3,+∞);
当-2<x≤1时,y∈(3,6];
当x>1时,y∈[6,+∞).
综上,y=f(x)的最小值是3.
(2)f(x)=|x-1|+|2x+4|.
令g(x)=f(x)-6=$\left\{\begin{array}{l}{-3x-9,x≤-2}\\{x-1,-2<x≤1}\\{3x-3,x>1}\end{array}\right.$,
①$\left\{\begin{array}{l}{x≤-2}\\{|-3x-9|≤1}\end{array}\right.$解得:x∈[-$\frac{10}{3}$,-$\frac{8}{3}$],
②$\left\{\begin{array}{l}{-2<x≤1}\\{|x-1|≤1}\end{array}\right.$解得:x∈[0,1],
③$\left\{\begin{array}{l}{x>1}\\{|3x-3|≤1}\end{array}\right.$解得:x∈(1,$\frac{4}{3}$].
综上,不等式|f(x)-6|≤1的解集为:[-$\frac{10}{3}$,-$\frac{8}{3}$]∪[0,1]∪(1,$\frac{4}{3}$]=[-$\frac{10}{3}$,-$\frac{8}{3}$]∪[0,$\frac{4}{3}$].
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
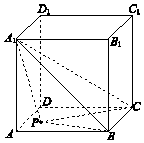 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.
如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com