
已知椭圆
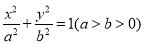 上的点到椭圆右焦点
上的点到椭圆右焦点 的最大距离为
的最大距离为 ,离心率
,离心率 ,直线
,直线 过点
过点 与椭圆
与椭圆 交于
交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2) 上是否存在点
上是否存在点 ,使得当
,使得当 绕
绕 转到某一位置时,有
转到某一位置时,有 成立?若存在,求出所有点
成立?若存在,求出所有点 的坐标与
的坐标与 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1)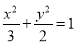 ;(2)
;(2)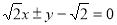 .
.
【解析】
试题分析:(1)设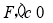 ,椭圆
,椭圆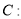
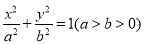 上的点到椭圆右焦点
上的点到椭圆右焦点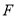 的最大距离为
的最大距离为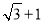 ,离心率
,离心率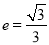 ,可得
,可得 求得a和b;(2)由(1)可得椭圆的方程,设A(x1,y1)、B(x2,y2),(ⅰ) 当
求得a和b;(2)由(1)可得椭圆的方程,设A(x1,y1)、B(x2,y2),(ⅰ) 当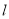 垂直于
垂直于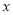 轴时,由
轴时,由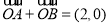 知,C上不存在点P使
知,C上不存在点P使 成立;(ⅱ)当l不垂直x轴时,设l的方程为y=k(x-1),代入椭圆的方程中整理得方程△>0.由韦达定理可求得
成立;(ⅱ)当l不垂直x轴时,设l的方程为y=k(x-1),代入椭圆的方程中整理得方程△>0.由韦达定理可求得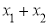 和
和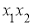 的表达式,假设存在点P,使
的表达式,假设存在点P,使 成立,则其充要条件为:点P的坐标为(x1+x2,y1+y2),代入椭圆方程;把A,B两点代入椭圆方程,最后联立方程求得c,进而求得P点坐标,因为
成立,则其充要条件为:点P的坐标为(x1+x2,y1+y2),代入椭圆方程;把A,B两点代入椭圆方程,最后联立方程求得c,进而求得P点坐标,因为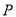 在椭圆上,
在椭圆上,
将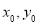 代入椭圆方程,得
代入椭圆方程,得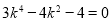 ,即可求出k的值和P的坐标以及l的方程.
,即可求出k的值和P的坐标以及l的方程.
【解析】
(1)由条件知 ,解得
,解得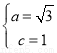 ,
,
所以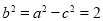 ,故椭圆方程为
,故椭圆方程为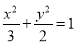 .
.
(2)C上存在点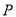 ,使得当
,使得当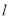 绕
绕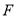 转到某一位置时,有
转到某一位置时,有 成立.
成立.
由(Ⅰ)知C的方程为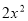 +
+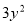 =6.设
=6.设
(ⅰ)当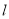 垂直于
垂直于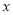 轴时,由
轴时,由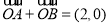 知,C上不存在点P使
知,C上不存在点P使 成立.
成立.
(ⅱ)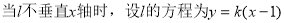
将 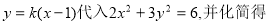
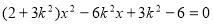
于是  ,
, 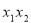 =
=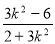 ,
,
C 上的点P使 成立的充要条件是
成立的充要条件是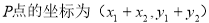 ,
,
设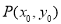 ,则
,则
所以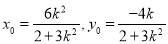 .因为
.因为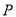 在椭圆上,
在椭圆上,
将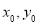 代入椭圆方程,得:
代入椭圆方程,得: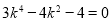 ,所以
,所以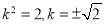 ,
,
当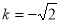 时,
时,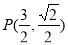 ,
, 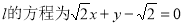 ;
;
当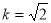 时,
时,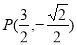 ,
, 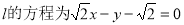 .
.
综上,C上存在点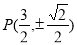 使
使 成立,
成立,
此时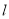 的方程为
的方程为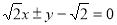 .
.
考点:1.直线与圆锥曲线的关系;2.椭圆的标准方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
下列四个函数,在x=0处取得极值的函数是( )
①y=x3 ②y=x2+1 ③y=|x| ④y=2x
A.①② B.②③ C.③④ D.①③
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
若过点 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线 斜率的取值范围为( )
斜率的取值范围为( )
A.[- ,
, ] B.(-
] B.(- ,
, ) C.
) C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二下学期期中检测文科数学试卷(解析版) 题型:选择题
椭圆
 的一个焦点为
的一个焦点为 ,若椭圆上存在一个点
,若椭圆上存在一个点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com