
 从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和.
从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和.分析 (1)由题意得:第四组有10名,第五组有6名,第七组有4名,第八组有2名,从而前三组共有24名,进而第一组有6名,第二组8名,第三组10名,由此作出频率分布直方图,估计该校1000名学生中成绩在120分以上(含120分)的人数.
(2)记第四组4名学生为a,b,c,d,第八组2名学生为E,F,由此利用列举法能求出事件G=||x-y|≤5|的概率P(G).
解答 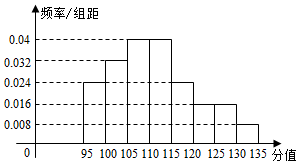 解:(1)由题意得:第四组有10名,第五组有6名,第七组有4名,第八组有2名,
解:(1)由题意得:第四组有10名,第五组有6名,第七组有4名,第八组有2名,
则前三组共有24名,
前三组的人数成等差数列,第一组有6名,
∴第二组8名,第三组10名,
由此作出频率分布直方图,如右图.
由频率分布直方图得成绩在120分以上(含120分)的频率为:(0.016+0.016+0.008)×5=0.2,
估计该校1000名学生中成绩在120分以上(含120分)的人数为:1000×0.2=200人.
(2)记第四组4名学生为a,b,c,d,
第八组2名学生为E,F,
所有学生中随机抽取两名学生有ab,ac,ad,aE,aF,bc,bd,bE,bF,cd,cE,cF,dE,dF,EF,共15种情况,
而事件G含有ab,ac,ad,bc,bd,cd,EF共7种情况,
∴事件G=||x-y|≤5|的概率P(G)=$\frac{7}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
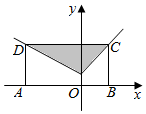 如图,在矩形ABCD中,点A在x轴上,点B的坐标为(2,0)且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率为$\frac{1}{3}$.
如图,在矩形ABCD中,点A在x轴上,点B的坐标为(2,0)且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com