
分析 (1)已知等式利用正弦定理化简,根据sinB不为0求出sinA的值,再由A为锐角,利用特殊角的三角函数值即可求出A的度数.
(2)因为b+c=4,利用基本不等式,可求得bc≤4,从而可求△ABC的面积的最大值.
解答 (本题满分为14分)
解:(1)利用正弦定理化简已知等式得:2sinAsinB=$\sqrt{3}$sinB,
∵sinB≠0,
∴sinA=$\frac{\sqrt{3}}{2}$,
∵A为锐角,
∴A=60°. …(7分)
(2)由基本不等式得,∵b+c=4≥2$\sqrt{bc}$,(当且仅当b=c=2,不等式等号成立).
∴bc≤4,…(10分)
∴S△ABC=$\frac{1}{2}$bcsinA≤$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴△ABC的面积的最大值为$\sqrt{3}$. …(14分)
点评 本题的考点是解三角形,主要考查正弦定理的应用,考查三角形的面积公式,基本不等式的运用,知识点多,计算需要细心,属于基础题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
 从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和.
从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$|<|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$=$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
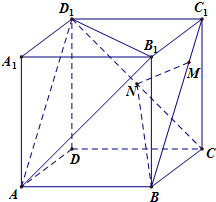 如图,正方体ABCD-A1B1C1D1的棱长为1,N为CD1中点,M为线段BC1上的动点,(M不与B,C1重合)有四个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,N为CD1中点,M为线段BC1上的动点,(M不与B,C1重合)有四个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com