Question

9．在四边形ABCD中，已知AB=9，BC=6，$\overrightarrow{CP}$=2$\overrightarrow{PD}$．
（1）若四边形ABCD是平行四边形，且$\overrightarrow{AP}$•$\overrightarrow{BP}$=18，求证：四边形ABCD是矩形；
（2）若$\overrightarrow{AB}$与$\overrightarrow{AD}$夹角的余弦值为$\frac{1}{3}$，且$\overrightarrow{AP}$•$\overrightarrow{BP}$∈[5，10]，用反证法证明：四边形ABCD不可能是平行四边形．

Answer 1

分析 （1）把$\overrightarrow{AB}、\overrightarrow{AD}$看作基底，把且$\overrightarrow{AP}$、$\overrightarrow{BP}$用基底表示，代入且$\overrightarrow{AP}$•$\overrightarrow{BP}$=18可得$\overrightarrow{AB}•\overrightarrow{AD}=0$，从而证得答案；
（2）假设四边形ABCD不可能是平行四边形，由已知结合平面向量的数量积运算求得$\overrightarrow{AP}$•$\overrightarrow{BP}$的范围，与已知范围矛盾，说明假设错误．

解答 证明：（1）如图
AB=9，BC=6，$\overrightarrow{CP}$=2$\overrightarrow{PD}$，且四边形ABCD是平行四边形，
由$\overrightarrow{AP}$•$\overrightarrow{BP}$=18，得$（\overrightarrow{AD}+\overrightarrow{DP}）•（\overrightarrow{BC}+\overrightarrow{CP}）$=$（\overrightarrow{AD}+\frac{1}{3}\overrightarrow{AB}）•（\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AB}）$=18，
即$|\overrightarrow{AD}{|}^{2}-\frac{1}{3}\overrightarrow{AB}•\overrightarrow{AD}-\frac{2}{9}|\overrightarrow{AB}{|}^{2}=18$，
∴36-$\frac{1}{3}\overrightarrow{AB}•\overrightarrow{AD}-18=18$，得$\overrightarrow{AB}•\overrightarrow{AD}=0$，
即AB⊥AD，
∴平行四边形ABCD是矩形；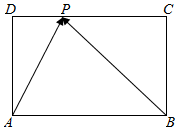
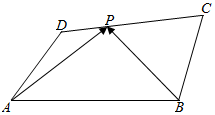
（2）如图，
假设四边形ABCD是平行四边形，
由AB=9，BC=6，$\overrightarrow{CP}$=2$\overrightarrow{PD}$，四边形ABCD是平行四边形，且cos＜$\overrightarrow{AB}，\overrightarrow{AD}$＞=$\frac{1}{3}$，
则$\overrightarrow{AP}$•$\overrightarrow{BP}$=$（\overrightarrow{AD}+\overrightarrow{DP}）•（\overrightarrow{BC}+\overrightarrow{CP}）$=$（\overrightarrow{AD}+\frac{1}{3}\overrightarrow{AB}）•（\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AB}）$=$|\overrightarrow{AD}{|}^{2}-\frac{1}{3}|\overrightarrow{AB}||\overrightarrow{AD}|×\frac{1}{3}-\frac{2}{9}|\overrightarrow{AB}{|}^{2}$
=$36-\frac{1}{3}×\frac{1}{3}×9×6-\frac{2}{9}×81$=12．
与已知$\overrightarrow{AP}$•$\overrightarrow{BP}$∈[5，10]矛盾，
∴假设错误，
故四边形ABCD不可能是平行四边形．

点评 本题考查平面向量的数量积运算，考查了向量加法与减法的几何意义，训练了反证法证题的思想和步骤，属中档题．