
分析 (1)定义Mα={ω|ω=α2n-1,n∈N+},且集合M中只有三个元素,可得α=α7,α≠0,即α6=1,解出即可得出.
(2)由x+$\frac{1}{x}$=$\sqrt{2}$,化为:x2-$\sqrt{2}$x+1=0,利用求根公式解得x,即可得出M.
解答 解:(1)∵定义Mα={ω|ω=α2n-1,n∈N+},且集合M中只有三个元素,
∴α=α7,α≠0,
∴α6=1,
取α=$cos\frac{π}{3}+isin\frac{π}{3}$=$\frac{1}{2}+\frac{\sqrt{3}}{2}i$.
∴Mα={$\frac{1}{2}+\frac{\sqrt{3}}{2}i$,-1,$\frac{1}{2}-\frac{\sqrt{3}}{2}i$}.
(2)由x+$\frac{1}{x}$=$\sqrt{2}$,化为:x2-$\sqrt{2}$x+1=0,解得x=$\frac{\sqrt{2}±\sqrt{2}i}{2}$,∴M=$\{\frac{\sqrt{2}+\sqrt{2}i}{2},\frac{\sqrt{2}-\sqrt{2}i}{2}\}$.
点评 本题考查了集合的运算性质、新定义、复数的运算性质、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数 | B. | x=$-\frac{π}{4}$是f(x)一条对称轴 | ||
| C. | f(x)的最小正周期为$\frac{π}{2}$ | D. | ($-\frac{π}{4}$,0)是f(x)的一条对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
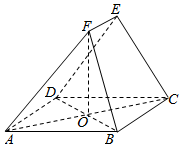 如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.
如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com