
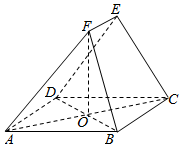
 如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.
如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=60°,对角线AC与BD相交于O;OF⊥平面ABCD,BC=CE=DE=2EF=2.分析 (Ⅰ)证明AD∥BC,即可证明BC∥面ADEF,然后证明EF∥BC.
(Ⅱ)以O为坐标原点,OA,OB,OF分别为x轴,y轴,z轴,建立空间直角坐标系,取CD的中点M,连OM,EM.易证EM⊥平面ABCD.求出设面BCFE的法向量,设$\overrightarrow{DF}$与$\overrightarrow{n_0}$所成角为φ,直线DE与面BCEF所成角为θ.通过sinθ=|cosφ|,求解直线EF与平面BCEF所成角的正弦值即可.
解答 解:(Ⅰ)因为四边形ABCD为菱形
所以AD∥BC,且BC?面ADEF,AD?面ADEF
所以BC∥面ADEF且面ADEF∩面BCEF=EF
所以EF∥BC.-----------------------------(6分)
(Ⅱ)因为FO⊥面ABCD
所以FO⊥AO,FO⊥OB
又因为OB⊥AO
以O为坐标原点,OA,OB,OF分别为x轴,y轴,z轴,建立空间直角坐标系,
取CD的中点M,连OM,EM.易证EM⊥平面ABCD.
又因为BC=CE=DE=2EF=2,得出以下各点坐标:$B(0,1,0),C(-\sqrt{3},0,0),D(0,-1,0),F(0,0,\sqrt{3}),E(-\frac{{\sqrt{3}}}{2},-\frac{1}{2},\sqrt{3})$
向量$\overrightarrow{DE}=(-\frac{{\sqrt{3}}}{2},\frac{1}{2},\sqrt{3})$,向量$\overrightarrow{BC}=(-\sqrt{3},-1,0)$,向量$\overrightarrow{BF}=(0,-1,\sqrt{3})$
设面BCFE的法向量为:$\overrightarrow{n_0}=({x_0},{y_0},{z_0})$,$\left\{\begin{array}{l}{\overrightarrow{{n}_{0}}•\overrightarrow{BC}=0}\\{\overrightarrow{{n}_{0}}•\overrightarrow{BF}=0}\end{array}\right.$,得到$\left\{\begin{array}{l}-\sqrt{3}{x_0}-{y_0}=0\\-{y_0}+\sqrt{3}{z_0}=0\end{array}\right.$
令${y_0}=\sqrt{3}$时$\overrightarrow{n_0}=(-1,\sqrt{3},1)$
设$\overrightarrow{DF}$与$\overrightarrow{n_0}$所成角为φ,直线DE与面BCEF所成角为θ.sinθ=|cosφ|=$\frac{{|\overrightarrow{n_0}•\overrightarrow{DE}|}}{{|\overrightarrow{n_0}|•|\overrightarrow{DE}|}}$=$\frac{{|(-\frac{{\sqrt{3}}}{2})×(-1)+\frac{1}{2}×\sqrt{3}+\sqrt{3}×1|}}{{\sqrt{{{(-1)}^2}+{{(\sqrt{3})}^2}+{{(1)}^2}}•\sqrt{{{(\frac{{-\sqrt{3}}}{2})}^2}+{{(\frac{1}{2})}^2}+{{(\sqrt{3})}^2}}}}$=$\frac{{\sqrt{15}}}{5}$
直线EF与平面BCEF所成角的正弦值为$\frac{{\sqrt{15}}}{5}$.-----------------------(13分)
点评 本题考查直线与平面平行的性质定理的应用,直线与平面所成角的求法,考查计算能力.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为矩形,且AB=1,AD=2,PA⊥平面ABCD,E、F为BC、AB的中点.
如图,四边形ABCD为矩形,且AB=1,AD=2,PA⊥平面ABCD,E、F为BC、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| t | 0 | t0 | 2t0 | 3t0 | 4t0 | 5t0 | 6t0 | 7t0 | 8t0 | 9t0 | 10t0 | 11t0 | 12t0 |
| y | -20.0 | -17.8 | -10.1 | 0.1 | 10.3 | 17.1 | 20.0 | 17.7 | 10.3 | 0.1 | -10.1 | -17.8 | -20.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
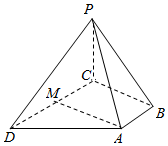 如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.
如图:四棱锥P-ABCD中,PD=PC,底面ABCD是直角梯形AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com