
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)是否存在一个奇数![]() ,使得数列
,使得数列![]() 中的项都在数列
中的项都在数列![]() 中?若存在,找出符合条件的一个奇数
中?若存在,找出符合条件的一个奇数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() (2)存在;
(2)存在;![]()
【解析】
(1)利用 将原递推公式进行化简,可得
将原递推公式进行化简,可得![]() ,进而可得
,进而可得![]() ,两式相减可得
,两式相减可得![]() ,再根据等差数列的定义可得数列
,再根据等差数列的定义可得数列![]() 和
和![]() 分别是以
分别是以![]() 为首项,
为首项,![]() 为公差的等差数列,由此即可求出结果;
为公差的等差数列,由此即可求出结果;
(2)当![]() 时,由
时,由![]() 可得
可得![]() ,
,![]() ,所以数列
,所以数列![]() 和
和![]() 分别是以
分别是以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,![]() 和
和![]() ,记
,记![]() ,当
,当![]() 为奇数时,
为奇数时,![]() 为奇数,而
为奇数,而![]() 为偶数;所以
为偶数;所以![]() 不是数列
不是数列![]() 中的项,
中的项,![]() 只可能是
只可能是![]() 中的项;若
中的项;若![]() 是数列
是数列![]() 中的项,由
中的项,由![]() ,得
,得![]() ,取
,取![]() ,得
,得![]() ,此时
,此时![]() ,由
,由![]() 得
得![]() ,即可求出结果.
,即可求出结果.
(1)当![]() 时,由已知得
时,由已知得![]()
于是![]()
由![]() 得:
得:![]()
于是![]()
由![]() 得:
得:![]()
由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,又
,又![]()
所以数列![]() 和
和![]() 分别是以
分别是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
![]() ,即
,即![]() 时,
时,![]()
![]() ,即
,即![]() 时,
时,![]()
∴![]()
(2)当![]() 时,由
时,由![]() 可得
可得![]() ,
,![]()
所以数列![]() 和
和![]() 分别是以
分别是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
![]()
![]()
由题设知,记![]() ,当
,当![]() 为奇数时,
为奇数时,![]() 为奇数,而
为奇数,而![]() 为偶数
为偶数
![]() 不是数列
不是数列![]() 中的项,
中的项,![]() 只可能是
只可能是![]() 中的项
中的项
若![]() 是数列
是数列![]() 中的项,由
中的项,由![]() ,得
,得![]()
取![]() ,得
,得![]() ,此时
,此时![]()
由![]() 得
得![]() ,即
,即![]()
故![]() 是数列
是数列![]() 中的第
中的第![]() 项
项
【点精】
本题主要考查了等差数列和等比数列的定义和性质,同时也考查了数列递推公式的应用,本题属于中档题.


科目:高中数学 来源: 题型:
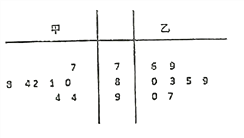
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示
(Ⅰ)计算:①甲地被抽取的观众评分的中位数;
②乙地被抽取的观众评分的极差;
(Ⅱ)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行评分调查,记抽取的4人评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)从甲、乙两地分别抽取的8名观众中各抽取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被抽取的观众评分低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
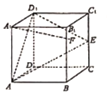
【题目】如图所示,在正方体![]() 中,E是棱
中,E是棱![]() 的中点,F是侧面内
的中点,F是侧面内![]() 的动点,且
的动点,且![]() 平面
平面![]() ,给出下列命题:
,给出下列命题:
![]() 点F的轨迹是一条线段;
点F的轨迹是一条线段;![]() 与
与![]() 不可能平行;
不可能平行;![]() 与BE是异面直线;
与BE是异面直线;![]() 平面
平面![]() 不可能与平面
不可能与平面![]() 平行.
平行.
其中正确的个数是![]()
![]()
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年冬季青奥会即将在瑞士盛大开幕,为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
选手 次数 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲 | 7.4 | 8.1 | 8.6 | 8.0 | 7.9 |
乙 | 7.8 | 8.4 | 7.6 | 8.1 | 8.1 |
A.甲,0.148B.乙,0.076C.甲,![]() D.乙,
D.乙,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P为曲线C上任意一点, ![]() ,直线
,直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求曲线![]() 的轨迹方程;;
的轨迹方程;;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com