
分析 (1)先求出A,B的坐标,再利用两点式求方程;
(2)利用两点间的距离公式,即可求出A,B两点间的距离|AB|
(3)AB的中点坐标为(1,0),直线AB的斜率为-$\frac{1}{2}$,即可求出直线AB的垂直平分线的方程.
解答 解:两圆方程联立,解方程组,可得A(3,-1),B(-1,1)
(1)直线AB的方程:y+1=$\frac{1+1}{-1-3}$(x-3),即x+2y-1=0;
(2)A,B两点间的距离|AB|=$\sqrt{(3+1)^{2}+(-1-1)^{2}}$=2$\sqrt{10}$;
(3)AB的中点坐标为(1,0),直线AB的斜率为-$\frac{1}{2}$,
∴直线AB的垂直平分线的方程2x-y-2=0.
点评 本题考查圆与圆的位置关系,考查直线方程,距离的计算,考查学生的计算能力,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
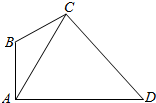 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25人 | B. | 15 人 | C. | 30 人 | D. | 20人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
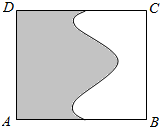 如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.
如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
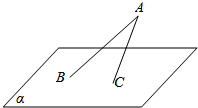 如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.
如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com