
分析 (1)设M(x,y),利用封闭曲线C上的任意点M与两定点O(0,0),P(0,3)的距离之比为2,可得封闭曲线C的方程;
(2)①求出切线方程,可得D,E的坐标,即可求|DE|的长度;
②设存在点N(x0,y0)满足条件,设过点N且与圆O相切的直线方程为:y-y0=k(x-x0)通过点到直线的距离公式,求出直线NA,NB的斜率分别为k1,k2的关系,通过圆C在点N处的切线方程,求出切线与x轴的交点坐标,D,E的坐标,然后利用斜率关系式求出点N的纵坐标.
解答 解:(1)设M(x,y),则
∵封闭曲线C上的任意点M与两定点O(0,0),P(0,3)的距离之比为2,
∴$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{{x}^{2}+(y-3)^{2}}}$=2
∴x2+(y-4)2=4;
(2)①设切线方程为y-5=k(x-$\sqrt{3}$),即kx-y+5-$\sqrt{3}$k=0,
∴$\frac{|5-\sqrt{3}k|}{\sqrt{{k}^{2}+1}}$=1,
∴k=$\sqrt{3}$或4$\sqrt{3}$,
k=$\sqrt{3}$,令y=0,可得x=-$\frac{2}{\sqrt{3}}$;k=4$\sqrt{3}$,令y=0,可得x=$\frac{7}{4\sqrt{3}}$;
∴|DE|=$\frac{7}{4\sqrt{3}}$+$\frac{2}{\sqrt{3}}$=$\frac{5\sqrt{3}}{4}$;
②设存在点N(x0,y0)满足条件
设过点N且与圆O相切的直线方程为:y-y0=k(x-x0)
则由题意得,$\frac{|-k{x}_{0}+{y}_{0}|}{\sqrt{1+{k}^{2}}}$=1,化简得$({{x}_{0}}^{2}-1){k}^{2}-2{x}_{0}{y}_{0}k+{{y}_{0}}^{2}-1=0$
设直线NA,NB的斜率分别为k1,k2,则k1+k2=$\frac{2{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-1}$,k1k2=$\frac{{{y}_{0}}^{2}-1}{{{x}_{0}}^{2}-1}$
圆C在点N处的切线方程为y-y0=$\frac{-{x}_{0}}{{y}_{0}-4}$(x-x0)
令y=0,得切线与x轴的交点坐标为($\frac{{{y}_{0}}^{2}-4{y}_{0}}{{x}_{0}}+{x}_{0}$,0)
又得D,E的坐标分别为($\frac{-{y}_{0}}{{k}_{1}}+{x}_{0}$,0),($\frac{-{y}_{0}}{{k}_{2}}+{x}_{0}$,0)
由题意知,2(($\frac{{{y}_{0}}^{2}-4{y}_{0}}{{x}_{0}}+{x}_{0}$)=$\frac{-{y}_{0}}{{k}_{1}}+{x}_{0}$+$\frac{-{y}_{0}}{{k}_{2}}+{x}_{0}$
用韦达定理代入可得,$\frac{{y}_{0}-4}{{x}_{0}}=\frac{-{x}_{0}{y}_{0}}{{{y}_{0}}^{2}-1}$,与x02+(y0-4)2=4联立,
得y0=$\frac{13+\sqrt{105}}{8}$.
点评 本题考查圆的方程,直线与圆的位置关系,点到直线的距离公式的应用,圆的切线方程的应用,考查分析问题解决问题的能力.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
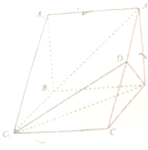 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com