
分析 (1)利用椭圆Q的长轴长为$2\sqrt{2}$,求出$a=\sqrt{2}$.设P(x0,y0),通过直线PA与OM的斜率之积恒为$-\frac{1}{2}$,化简求出b,即可得到椭圆方程.
(2)设直线l方程为y=k(x+1)(k≠0),代入$\frac{x^2}{2}+{y^2}=1$有(1+2k2)x2+4k2x+2k2-2=0,设A(x1,y1),B(x2,y2),AB中点N(x0,y0),利用韦达定理求出CD的垂直平分线方程,推出${x_G}={x_0}+k{y_0}=-\frac{1}{2}+\frac{1}{{4{k^2}+2}}$,利用弦长公式化简,推出|CD|的最小值.
解答 解:(1)∵椭圆Q的长轴长为$2\sqrt{2}$,∴$a=\sqrt{2}$.
设P(x0,y0),
∵直线PA与OM的斜率之积恒为$-\frac{1}{2}$,∴$\frac{{\frac{y_0}{2}}}{{\frac{{{x_0}+\sqrt{2}}}{2}}}×\frac{y_0}{{{x_0}-\sqrt{2}}}=-\frac{1}{2}$,
∴$\frac{x_0^2}{2}+y_0^2=1$,∴b=1,
故椭圆的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)设直线l方程为y=k(x+1)(k≠0),代入$\frac{x^2}{2}+{y^2}=1$有(1+2k2)x2+4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),AB中点N(x0,y0),
∴$({x_1}+{x_2})=-\frac{{4{k^2}}}{{1+2{k^2}}},{x_1}•{x_2}=\frac{{2{k^2}-2}}{{1+2{k^2}}}$.
∴${x_0}=\frac{1}{2}({x_1}+{x_2})=-\frac{{2{k^2}}}{{1+2{k^2}}},{y_0}=k({x_0}+1)=\frac{k}{{1+2{k^2}}}$
∴CD的垂直平分线方程为$y-{y_0}=-\frac{1}{k}(x-{x_0})$,
令y=0,得${x_G}={x_0}+k{y_0}=-\frac{1}{2}+\frac{1}{{4{k^2}+2}}$
∵${x_G}∈[-\frac{1}{4},0)$,∴$-\frac{1}{4}≤-\frac{1}{2}+\frac{1}{{4{k^2}+2}}$,∴$0<{k^2}≤\frac{1}{2}$.$|CD|=\sqrt{1+{k^2}}|{x_2}-{x_1}|=\sqrt{1+{k^2}}•\frac{{\sqrt{16{k^4}-4(2{k^2}+1)(2{k^2}-2)}}}{{2{k^2}+1}}$=$2\sqrt{2}[\frac{1}{2}+\frac{1}{{2(2{k^2}+1)}}]≥\frac{{3\sqrt{2}}}{2}$,$|CD{|_{min}}=\frac{{3\sqrt{2}}}{2}$.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的应用,弦长公式的应用,设而不求的思想方法,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2},1)$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
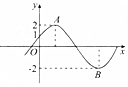 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,则函数g(x)=2cos(φx+ω)图象的对称轴为( )| A. | x=12k-8(k∈Z) | B. | x=6k-2(k∈Z) | C. | x=6k-4(k∈Z) | D. | x=12k-2(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com