
| A. | (-∞,0) | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2},1)$ | D. | (1,+∞) |
分析 通过变形可知问题转化为不等式f(x1)-f(1-x1)>f(1)-f(1-1)恒成立,设g(x)=f(x)-f(1-x)并求导可知g(x)在R上单调递增,利用单调性即得结论.
解答 解:∵不等式f(x1)+f(0)>f(x2)+f(1)恒成立,
∴不等式f(x1)-f(x2)>f(1)-f(0)恒成立,
又∵x1+x2=1,
∴不等式f(x1)-f(1-x1)>f(1)-f(1-1)恒成立,
设g(x)=f(x)-f(1-x),
∵f(x)=ex+mx2-m(m>0),
∴g(x)=ex-e1-x+m(2x-1),
则g′(x)=ex+e1-x+2m>0,∴g(x)在R上单调递增,
∴不等式g(x1)>g(1)恒成立,
∴x1>1,
故选:D.
点评 本题是一道关于导数的综合题,考查转化与化归思想,构造新函数是解决本题的关键,注意解题方法的积累,属于难题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩 编号 | 1 | 2 | 3 | 4 | 5 |
| 物理(x) | 90 | 85 | 74 | 68 | 63 |
| 数学(y) | 130 | 125 | 110 | 95 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
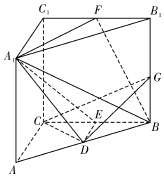 如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{22}{17}$ | B. | $\frac{22}{17}$i | C. | $\frac{22}{17}$ | D. | $\frac{3}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},1)$ | B. | $(\frac{1}{2},\frac{3}{4})$ | C. | $(\frac{1}{3},1)$ | D. | $(\frac{1}{2},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com