
【题目】关于曲线![]() ,给出下列四个结论:
,给出下列四个结论:
①曲线C关于原点对称,但不关于x轴、y轴对称;
②曲线C恰好经过4个整点(即横、纵坐标均为整数的点);
③曲线C上任意一点都不在圆![]() 的内部;
的内部;
④曲线C上任意一点到原点的距离都不大于![]() .
.
其中,正确结论的序号是________.
【答案】①④
【解析】
根据关于原点、x轴、y轴对称的横纵坐标特点,代入即可判断①;取![]() 的整数值,代入求得
的整数值,代入求得![]() 的值即可判断②;由基本不等式确定
的值即可判断②;由基本不等式确定![]() 的最大值,即可判断③;由两点间距离公式及基本不等式,化简即可判断④;
的最大值,即可判断③;由两点间距离公式及基本不等式,化简即可判断④;
曲线![]() ,
,
对于①,将![]() 替换
替换![]() ,
,![]() 替换
替换![]() ,代入可得
,代入可得![]() ,所以曲线C关于原点对称;
,所以曲线C关于原点对称;
将![]() 替换
替换![]() ,代入可得
,代入可得![]() ,所以曲线C不关于y轴对称;
,所以曲线C不关于y轴对称;
将![]() 替换
替换![]() ,代入可得
,代入可得![]() ,所以曲线C不关于
,所以曲线C不关于![]() 轴对称;所以①正确;
轴对称;所以①正确;
对于②,当![]() 时,代入可得
时,代入可得![]() ,所以经过
,所以经过![]() ;
;
当![]() 时,代入可得
时,代入可得![]() ,所以经过
,所以经过![]() ;
;
当![]() 时,代入可得
时,代入可得![]() ,所以经过
,所以经过![]() ;
;
当![]() 时,代入可得
时,代入可得![]() ,所以经过
,所以经过![]() ;
;
所以至少有六个整点在曲线C上,所以②错误;
对于③,由![]() 可知
可知![]() ,
,
而![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即![]() ,则
,则![]() ,
,
同理![]() ,解得
,解得![]() ,
,
所以![]() ,则③错误;
,则③错误;
对于④,由③可知![]() ,
,
所以![]() ,故④正确,
,故④正确,
综上可知,正确的为①④,
故答案为:①④.


科目:高中数学 来源: 题型:
【题目】某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段![]() 进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):
进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下):

(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一全年级中“体育良好”的学生人数;
(Ⅱ)为分析学生平时的体育活动情况,现从体育成绩在![]() 和
和![]() 的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在
的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在![]() 的概率;
的概率;
(Ⅲ)假设甲、乙、丙三人的体育成绩分别为![]() 且分别在
且分别在![]() 三组中,其中
三组中,其中![]() 当数据
当数据![]() 的方差
的方差![]() 最小时,写出
最小时,写出![]() 的值.(结论不要求证明)
的值.(结论不要求证明)
(注: ![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上的三个点,
上的三个点,![]() 为坐标原点.
为坐标原点.
(1)若![]() 所在的直线方程为
所在的直线方程为![]() ,求
,求![]() 的长;
的长;
(2)设![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,当
,当![]() 中点恰为点
中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
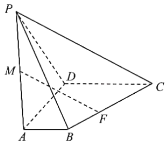
(I)求证:![]() ;
;
(II)求二面角_____的余弦值;
从①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
(III)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由![]() 个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由
个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由![]() 个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设
个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设![]() ,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
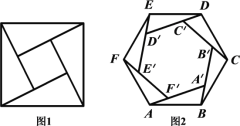
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: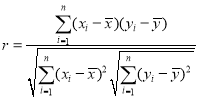 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com