
【题目】已知函数![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求a的值;
,求a的值;
(2)在(1)的条件下,若存在![]() ,使
,使![]() ,求t的取值范围.
,求t的取值范围.
【答案】(1)2;(2)![]() .
.
【解析】
(1)求得不等式f(x)<6的解集为a﹣3≤x≤3,再根据不等式f(x)<6的解集为(﹣1,3),可得a﹣3=﹣1,由此求得a的范围;
(2)令g(x)=f(x)+f(﹣x)=|2x﹣2|+|2x+2|+4,求出g(x)的最小值,可得t的范围.
(1)∵函数f(x)=|2x﹣a|+a,
不等式f(x)<6的解集为(﹣1,3),
∴|2x﹣a|<6﹣a 的解集为(﹣1,3),
由|2x﹣a|<6﹣a,可得a﹣6<2x+a<6﹣a,求得a﹣3≤x≤3,
故有a﹣3=﹣1,a=2.
(2)在(1)的条件下,f(x)=|2x﹣2|+2,
令g(x)=f(x)+f(﹣x)=|2x﹣2|+|2x+2|+4=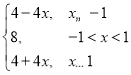
故g(x)的最小值为8,
故使f(x)≤t﹣f(﹣x)有解的实数t的范围为[8,+∞).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
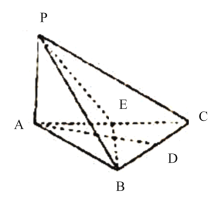
【题目】如图,三棱锥![]() 中,
中,![]() 底面
底面![]() 为等边三角形,
为等边三角形,![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)如何在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() 并说明理由;
并说明理由;
(3)若![]() ,对于(2)中的点
,对于(2)中的点![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
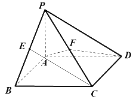
【题目】如图,在四棱锥![]() 中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
(1)求三棱锥![]() 的体积;
的体积;
(2)求直线EC与平面PCD所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海途安型号出租车价格规定:起步费![]() 元,可行
元,可行![]() 千米;
千米;![]() 千米以后按每千米按
千米以后按每千米按![]() 元计价,可再行
元计价,可再行![]() 千米;以后每千米都按
千米;以后每千米都按![]() 元计价。假如忽略因交通拥挤而等待的时间.
元计价。假如忽略因交通拥挤而等待的时间.
![]() 请建立车费
请建立车费![]() (元)和行车里程
(元)和行车里程![]() (千米)之间的函数关系式;
(千米)之间的函数关系式;
![]() 注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长
注意到上海出租车的计价系统是以元为单位计价的,如:小明乘坐途安型号出租车从华师大二附中本部到浦东实验学校走路线一(路线一总长![]() 千米)须付车费
千米)须付车费![]() 元,走路线二(路线二总长
元,走路线二(路线二总长![]() 千米)也须付车费
千米)也须付车费![]() 元.将上述函数解析式进行修正(符号
元.将上述函数解析式进行修正(符号![]() 表示不大于
表示不大于![]() 的最大整数,符号
的最大整数,符号![]() 表示不小于
表示不小于![]() 的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长
的最小整数);并求小明乘坐途安型号出租车从华师大二附中本部到闵行分校须付车费多少元?(注:两校区路线长![]() 千米)
千米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() .
.
(1)求以![]() 为焦点,原点为顶点的抛物线方程;
为焦点,原点为顶点的抛物线方程;
(2)若椭圆![]() 上点
上点![]() 满足
满足![]() ,求
,求![]() 的纵坐标
的纵坐标![]() ;
;
(3)设![]() ,若椭圆
,若椭圆![]() 上存在两个不同点
上存在两个不同点![]() 、
、![]() 满足
满足![]() ,证明:直线
,证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com