
【题目】已知函数 ![]() 在区间
在区间 ![]() 上有最大值
上有最大值 ![]() 和最小值
和最小值 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上有解,求实数
上有解,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:令t=2x∈[2,4], 则y=at2-2at+1-b,t∈[2,4],
对称轴t=1,a>0
∴t=2时,ymin=4a-4a+1-b=1, t=4时,ymax=16a-8a+1-b=9, 解得a=1,b=0
(2)解:4x-22x+1-k4x≥0在x∈[-1,1]上有解
设2x=t
∵x∈[-1,1],
∴t∈[ ![]() ,2]
,2]
∵f(2x)-k.2x≥0在x∈[-1,1]有解
∴t2-2t+1-kt2≥0在t∈[ ![]() ,2]有解
,2]有解
∴k≤ ![]() =1-
=1- ![]() +
+ ![]() ,
,
再令 ![]() =m,则m∈[
=m,则m∈[ ![]() ,2]
,2]
∴k≤m2-2m+1=(m-1)2
令h(m)=m2-2m+1
∴h(m)max=h(2)=1
∴k≤1
故实数k的取值范围(-∞,1]
【解析】(1)先换元,转化为一元二次函数在闭区间上的最值问题,利用一元二次函数的性质,求出顶点和闭区间端点的函数值,最大的即为最大值,最小的即为最小值。
(2)先换元,转化为t2-2t+1-kt2≥0在t∈[ 1 2 ,2]有解,求k的取值范围。将k移到不等式的一边,求出另一侧二次函数的最大值,即可得到k的取值范围,k≤(m-1)2在m∈[ ![]() ,2]有解,等价于在[
,2]有解,等价于在[ ![]() ,2],k要小于等于(m-1)2最大值。
,2],k要小于等于(m-1)2最大值。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若点O(0,0)和点 ![]() 分别是双曲线
分别是双曲线 ![]() ﹣y2=1(a>0)的中心和右焦点,A为右顶点,点M为双曲线右支上的任意一点,则
﹣y2=1(a>0)的中心和右焦点,A为右顶点,点M为双曲线右支上的任意一点,则 ![]() 的取值范围为( )
的取值范围为( )
A.[﹣1,+∞)
B.(0,+∞)
C.[﹣2,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=2,a3+a5=16. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)如果a2 , am , a2m成等比数列,求正整数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1 , M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD的体积为 ![]() ,其三视图如图所示,其中正视图为等腰 三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰 三角形,侧视图为直角三角形,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数( ) 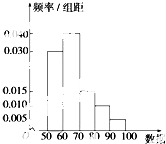
A.63、64、66
B.65、65、67
C.65、64、66
D.64、65、64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1 , y1),B(x2 , y2)均在抛物线上. 
(1)写出该抛物线的方程及其准线方程;
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com