【题目】在△ABC中， 
，求b，c．
【答案】解：∵ 
，sinA=sin120°= 
，
∴bc=4①，又cosA=cos120°=﹣ 
，且a= 
，
根据余弦定理a2=b2+c2﹣2bccosA得：21=b2+c2+bc=（b+c）2﹣bc，
即（b+c）2=25，开方得：b+c=5②，
而c＞b，联立①②，求得b=1，c=4．
【解析】由A的度数求出sinA的值，利用三角形的面积公式表示出三角形ABC的面积，使面积等于 
，把sinA的值代入可得bc的值，然后再求出cosA的值，由a的值及cosA的值，利用余弦定理表示出a2 ， 配方变形后，把bc及cosA的值代入，开方可得b+c的值，联立bc的值与b+c的值，即可求出b和c的值．
【考点精析】根据题目的已知条件，利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:
；余弦定理:
;
;
．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣ 
x+ 
，若数列{bn}满足：b1=1，bn+1=2f（bn）（n∈N*）．若对n∈N* ， 都M∈Z，使得 
＜M恒成立，则整数M的最小值是（ ）
A.2
B.3
C.4
D.5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD与BDEF均为菱形，设AC与BD相交于点O，若∠DAB=∠DBF=60°，且FA=FC． 
（1）求证：FC∥平面EAD；
（2）求直线AF与平面BCF所成角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥A﹣BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD= 
，AB=AC．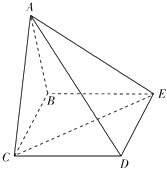 
（1）证明：AD⊥CE；
（2）设CE与平面ABE所成的角为45°，求二面角C﹣AD﹣E的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设命题p：方程x2+2mx+1=0有两个不相等的负根，命题q：x∈R，x2+2（m﹣2）x﹣3m+10≥0恒成立．
（1）若命题p、q均为真命题，求m的取值范围；
（2）若命题p∧q为假，命题p∨q为真，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某科技研究所对一批新研发的产品长度进行检测（单位：mm），如图是检测结果的频率分布直方图，据此估计这批产品的中位数为（ ） 
A.20
B.22.5
C.22.75
D.25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
