
| 学段 | 班 级 学生数 | 配 备 教师数 | 硬件建设 (万元) | 教师年薪 (万元) |
| 初中 | 40 | 2.5 | 25 | 3.2万元∕人 |
| 高中 | 45 | 4.0 | 50 | 4.0万元∕人 |
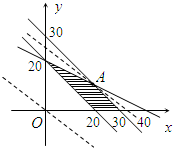 解:设开办初中班x个,高中班y个,收取的学费总额为z万元.
解:设开办初中班x个,高中班y个,收取的学费总额为z万元.| 7 |
| 9 |
| z |
| 36 |
| 7 |
| 9 |
| z |
| 36 |
|


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
 椭圆G的中心为原点O,A(4,0)为椭圆G的一个长轴端点,F为椭圆的左焦点,直线l经过点E(2,0),与椭圆G交于B、C两点,当直线l垂直x轴时,|BC|=6.
椭圆G的中心为原点O,A(4,0)为椭圆G的一个长轴端点,F为椭圆的左焦点,直线l经过点E(2,0),与椭圆G交于B、C两点,当直线l垂直x轴时,|BC|=6.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB⊥平面ABCD,且ED=FB=1.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| ||
| 2 |
| PQ |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,若aij=2013,则i与j的和为
如图,把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,若aij=2013,则i与j的和为查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com