
分析 (1)解不等式求出m的范围即可;(2)根据纯虚数的定义得到关于m的不等式组,解出即可.
解答 解:(1)由z的对应点在x轴上方,
得m2-2m-15>0,解得m<-3或m>5.
(2)因为$\frac{z}{1+i}=\frac{{z({1-i})}}{2}=\frac{{2{m^2}+3m-9}}{2}-\frac{7m+21}{2}i$,
由$\frac{z}{1+i}$为纯虚数,得$\left\{\begin{array}{l}\frac{{2{m^2}+3m-9}}{2}=0\\ \frac{7m+21}{2}≠0\end{array}\right.$,
解得$m=\frac{3}{2}$.
点评 本题考查了复数的定义,考查纯虚数问题,是一道基础题.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
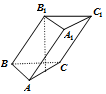 已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
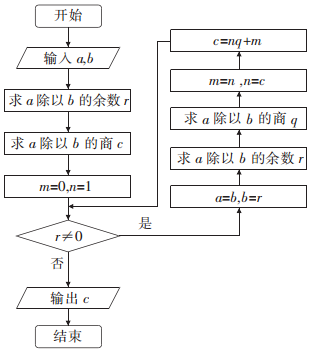
| A. | 7 | B. | 9 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com