练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．在△ABC中，若sinA：sinB：sinC=3：5：7，则cosC=-$\frac{1}{2}$．

    分析 由正弦定理可得a：b：c=3：5：7，进而可用b表示a，c，代入余弦定理化简可得．

    解答 解：∵sinA：sinB：sinC=3：5：7，
    ∴由正弦定理可得a：b：c=3：5：7，
    ∴a=$\frac{3b}{5}$，c=$\frac{7b}{5}$，
    由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{\frac{9{b}^{2}}{25}+{b}^{2}-\frac{49{b}^{2}}{25}}{2×\frac{3b}{5}×b}$=-$\frac{1}{2}$．
    故答案为：-$\frac{1}{2}$．

    点评 本题考查正、余弦定理的应用，用b表示a，c是解决问题的关键，考查了转化思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．求值：cos415°-sin415°=$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

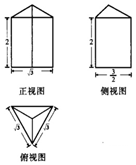    8．如图是由正三棱椎与正三棱柱组合而成的几何体的三视图，该几何体的顶点都在半径为R的球面上，则R=（　　）
    A．1B．$\sqrt{2}$C．$\frac{1+\sqrt{2}}{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某学校课题组为了研究学生的数学成绩与学生细心程度的关系，在本校随机调查了100名学生进行研究．研究结果表明：在数学成绩及格的60名学生中有45人比较细心，另15人比较粗心；在数学成绩不及格的40名学生中有10人比较细心，另30人比较粗心．
    （1）试根据上述数据完成2×2列联表；
    数学成绩及格数学成绩不及格合计
    比较细心451055
    比较粗心153045
    合计6040100
    （2）能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系．
    参考数据：独立检验随机变量K2的临界值参考表：
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    ${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．实数m分别取什么数值时，复数z=（m2+5m+6）+（m2-2m-15）i
    （1）对应的点在x轴的上方；
    （2）$\frac{z}{1+i}$为纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．△ABC内角A，B，C的对边分别为a，b，c，若a，b，c成等差数列，且sinA，sinB，sinC成等比数列，则角B=$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．△ABC的内角A，B，C的对边分别为，且2acosC=2b-c．
    （1）求A的大小；
    （2）若△ABC为锐角三角形，求sinB+sinC的取值范围；
    （3）若$a=2\sqrt{3}$，且△ABC的面积为$2\sqrt{3}$，求cos2B+cos2C的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知A是△BCD所在平面外一点，E、F分别是BC和AD的中点，若BD⊥AC，BD=AC，则EF与BD所成角的大小是45°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．双曲线$\frac{{x}^{2}}{m+5}$-$\frac{{y}^{2}}{20-m}$=1的焦距是（　　）
    A．4B．6C．10D．与m有关

    查看答案和解析>>

    同步练习册答案