
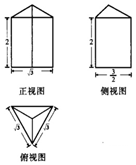
 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
分析 几何体外接球的球心在棱柱上下底面中心连线的中点,根据三棱柱的底面边长和高,利用勾股定理即可求出外接球半径.
解答  解:正三棱柱的底面边长为$\sqrt{3}$,三棱柱的高为2,
解:正三棱柱的底面边长为$\sqrt{3}$,三棱柱的高为2,
设正三棱柱的上下底面中心为O,O1,
则几何体外接球的球心为OO1的中点H,
设三棱柱的底面一个顶点为A,
∵底面边长为$\sqrt{3}$,∴O1A=$\frac{3}{2}×\frac{2}{3}$=1,O1H=1,
∴HA=$\sqrt{{O}_{1}{A}^{2}+{O}_{1}{H}^{2}}$=$\sqrt{2}$.
即外接球的半径为$\sqrt{2}$.
故选:B.
点评 本题考查了棱柱与外接球的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
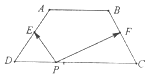 如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )
如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
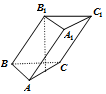 已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )
已知一三棱柱ABC-A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com