
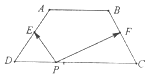
 如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )
如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |
分析 建立坐标系,设P的坐标,根据建立坐标系,设P的坐标,根据$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ得到λ关于x的方程,根据P的位置分四种情况讨论方程解得情况.
解答  解:以DC所在直线为x轴,DC的中垂线为y轴建立平面直角坐标系
解:以DC所在直线为x轴,DC的中垂线为y轴建立平面直角坐标系
则梯形的高为$\sqrt{5-1}$=2,∴A(-1,2),B(1,2),C(2,0),D(-2,0),∴E(-$\frac{3}{2}$,1),F($\frac{3}{2}$,1).
1)当P在DC上时,设P(x,0)(-2≤x≤2),则$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,1),$\overrightarrow{PF}$=($\frac{3}{2}$,1).
于是$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+1=x2-$\frac{5}{4}$=λ,
∴当λ=-$\frac{5}{4}$时,方程有一解,当-$\frac{5}{4}$<λ≤$\frac{11}{4}$时,λ有两解;
(2)当P在AB上时,设P(x,2)(-1≤x≤1),则$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,-1),$\overrightarrow{PF}$=($\frac{3}{2}$,-1).
∴$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+1=x2-$\frac{5}{4}$=λ,
∴当λ=-$\frac{5}{4}$时,方程有一解,当-$\frac{5}{4}$<λ≤-$\frac{1}{4}$时,λ有两解;
(3)当P在AD上时,直线AD方程为y=2x+4,
设P(x,2x+4)(-2<x<-1),则$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,-2x-3),$\overrightarrow{PF}$=($\frac{3}{2}$-x,-2x-3).
于是$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+(-2x-3)2=5x2+12x+$\frac{27}{4}$=λ.
∴当λ=-$\frac{9}{20}$或-$\frac{1}{4}$<λ<$\frac{9}{4}$时,方程有一解,当-$\frac{9}{20}$<λ<-$\frac{1}{4}$时,方程有两解;
(4)当P在CD上时,由对称性可知当λ=-$\frac{9}{20}$或-$\frac{1}{4}$<λ<$\frac{9}{4}$时,方程有一解,
当-$\frac{9}{20}$<λ<-$\frac{1}{4}$时,方程有两解;
综上,若使梯形上有8个不同的点P满足$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,
则λ的取值范围是(-$\frac{5}{4}$,$\frac{11}{4}$]∩(-$\frac{5}{4}$,-$\frac{1}{4}$]∩(-$\frac{9}{20}$,-$\frac{1}{4}$)∩(-$\frac{9}{20}$,-$\frac{1}{4}$)=(-$\frac{9}{20}$,-$\frac{1}{4}$).
故选D.
点评 本题考查了平面向量的数量积运算,二次函数与二次方程的关系,分类讨论思想,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
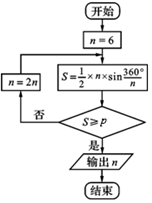 三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )
三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )| A. | 2.6 | B. | 3 | C. | 3.1 | D. | 3.14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
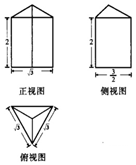 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com